Akademik

- оператор А: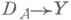 такой, что из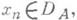 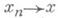и 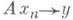следует 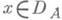и Ах=у (здесь X, Y- банаховы пространства над одним и тем же полем скаляров и - область определения оператора А). Понятие 3. о. распространяется и на операторы, действующие в отделимых линейных топологич. пространствах, только вместо последовательностей {х _п} надо рассматривать произвольные направления (сети) {х_x }. Если GrA- график оператора А, то Азамкнут тогда и только тогда, когда GrA есть замкнутое подмножество декартова произведения XY. Это свойство часто принимается за определение 3.о.

Понятие 3. о. есть обобщение понятия оператора, определенного и непрерывного на замкнутом подмножестве банахова пространства. Примером замкнутого, но не непрерывного оператора является оператор определенный на множестве С ₁[ а, b]непрерывно дифференцируемых функций пространства С[ а, b]. Замкнутыми, но не непрерывными являются многие операторы математич. физики.

Оператор Адопускает замыкание (т. е.- замыкаем), если существует замкнутое расширение этого оператора. Для того чтобы оператор был замыкаем, необходимо и достаточно, чтобы из 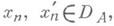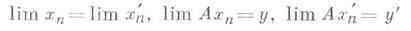следовало у=у'. Наименьшее замкнутое расширение оператора паз. его замыканием. Симметрический оператор в гильбертовом пространстве с плотной областью определения всегда допускает замыкание.

Линейный ограниченный оператор А:замкнут.

Обратно, если Аопределен на всем Xи замкнут, то он ограничен. Если Азамкнут и А ^-1 существует, то А ^-1 также замкнут. Так как А: замкнут тогда и только тогда, когда А-lI замкнут, то Азамкнут, если резольвента R_l (А)=(А-lI)^-1 существует и ограничена хотя бы для одного значения параметра lОС.

Если Dвсюду плотно в Xи, следовательно, однозначно определен сопряженный оператор А *: то А*- З. о. Если, кроме того, D_a* = Y и X, Y рефлексивны, то А- замыкаемый оператор и А * * является замыканием А.

3. о. Ас помощью введения новой нормы в области его определения можно сделать ограниченным. Пусть

Тогда D_A с новой нормой будет банаховым пространством и А, как оператор из (D _А|| Х ||₀) в У, будет ограниченным.

Лит.:[1] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [2] Като Т., Теория возмущений линейных операторов, пер. с англ., М., 1972.

В. И. Соболев