Akademik

объекта категории - понятие, аналогичное понятию подструктуры математич. структуры. Пусть - произвольная категория и А - фиксированный объект из . В классе всех мономорфизмов из 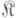с концом в Авводится отношение предпорядка (отношение делимости справа): предшествует или 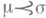, если m=m's для нек-рого 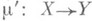. В действительности, морфизм m' однозначно определен, поскольку s - мономорфизм. Отношение предпорядка индуцирует отношение эквивалентности между мономорфизмами с концом в А:мономорфизмы и эквивалентны тогда и только тогда, когда и . Класс эквивалентных мономорфизмов наз. под объектом объекта А. П. с представителем иногда обозначают или (m]. Допускается также возможность с помощью т. н. символа t Гильберта произвести выбор представителей подобъектов объекта Аи рассматривать этих представителей в качестве подобъектов. В категориях множеств, групп, абелевых групп, векторных пространств П. любого объекта определяется канонич. вложением подмножества (подгруппы, подпространства) в объемлющее множество (группу, пространство). Однако в категории тополо-гич. пространств введенное понятие П. шире понятия подмножества с индуцированной топологией.

Отношение предпорядка между мономорфизмами с общим концом Аиндуцирует отношение порядка между П. объекта , если m<s. Это отношение аналогично отношению включения подмножеств некоторого множества.

Если мономорфизм m регулярен, то любой эквивалентный ему мономорфизм также регулярен. Поэтому можно говорить о регулярных П. любого объекта А. В частности, П. с представителем 1_A регулярен. В категориях с нулевыми морфизмами аналогично вводятся нормальные П. Если в категории существует бикатегорная структура , то подобъект (m:XА]объекта Аназ. допустимым (относительно указанной бикатегорной структуры), если .

М. Ш. Цаленко.