Akademik

в категории - морфизм категории 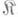, для к-рого из всякого равенства 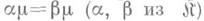следует, что (другими словами, на можно сокращать справа). Другое эквивалентное определение М.: для любого объекта Xкатегории 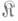индуцируемое морфизмом m отображение множеств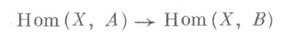

должно быть инъективным. Произведение двух М. является М. Каждый левый делитель М. есть М. Класс всех объектов и класс всех М. произвольной категории составляют подкатегорию категории (обозначаемую обычно ).

В категории множеств роль М. играют инъекции. Двойственным к понятию М. является понятие эпиморфизма.

Лит.:[1] Цаленко М. Ш., Шульгейфер Е. Г., Основы теории категорий, М., 1974; [2] Букур И., Деляну А., Введение в теорию категорий и функторов, пер. с англ., М., 1972.

О. А. Иванова.