Akademik

категории - термин, используемый для обозначения элементов произвольной категории, играющих роль отображений множеств друг в друга, гомоморфизмов групп, колец, алгебр, непрерывных отображений топологич. пространств и т. п. М. категории - неопределяемое понятие. Каждая категория состоит из элементов двух классов, наз. классом объектов и классом морфизмов соответственно. Класс М. категории 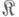обычно обозначается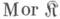

Любой М. aкатегории 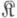имеет однозначно определенное начало - объект Аи однозначно определенный конец - объект В. Все М. с общими началом Аи концом Вобразуют подмножество 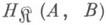класса 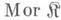. Тот факт, что М. 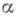имеет начало Аи конец В, можно записать обычным образом: 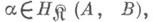пли с помощью стрелок: 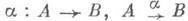и т. п.

Деление элементов категории на М. и объекты имеет смысл только в пределах фиксированной категории, т. к. М. одной категории могут быть объектами другой и наоборот. М. любой категории образуют систему, замкнутую относительно частичной бинарной операции - умножения. В зависимости от свойств М. по отношению к этой операции выделяются специальные классы М., напр, мономорфизм, эпиморфизм, биморфизм, изоморфизм, нулевой морфизм, нормальный мономорфизм, нормальный эпиморфизм и Т. Д. М. Ш. Цаленко.