- статистическая оценка, математич. ожидание к-рой совпадает с оцениваемой величиной. Пусть по реализации случайной величины X, принимающей значения в выборочном пространстве  надлежит оценить функцию
надлежит оценить функцию 
 , отображающую параметрич. множество
, отображающую параметрич. множество  в не-к-рое множество
в не-к-рое множество  , и пусть в качестве оценки функции
, и пусть в качестве оценки функции  выбрана статистика
выбрана статистика 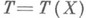 . Если статистич. оценка Ттакова, что равенство
. Если статистич. оценка Ттакова, что равенство

выполняется для всех  , то Тназ. несмещенной оценкой функции
, то Тназ. несмещенной оценкой функции  . Про Н. о. часто говорят, что она лишена систематич. ошибки.
. Про Н. о. часто говорят, что она лишена систематич. ошибки.
Пример 1. Пусть  - случайные величины, имеющие одно и то же математич. ожидание
- случайные величины, имеющие одно и то же математич. ожидание  , т. е.
, т. е.

В таком случае статистика

является Н. о. математич. ожидания  . В частности, среднее арифметическое наблюдений
. В частности, среднее арифметическое наблюдений 
 является Н. о. для q. В данном примере
является Н. о. для q. В данном примере  q
q
Пример 2. Пусть  - независимые случайные величины, подчиняющиеся одному и тому же вероятностному закону, функция распределения к-рого есть F(x), т. е.
- независимые случайные величины, подчиняющиеся одному и тому же вероятностному закону, функция распределения к-рого есть F(x), т. е.

В таком случае функция эмпирия, распределения  , построенная по наблюдениям
, построенная по наблюдениям  является Н. о. функции распределения F(x), т. е.
является Н. о. функции распределения F(x), т. е.
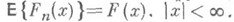
Пример 3. Пусть  - Н. о. параметра
- Н. о. параметра  , т. е.
, т. е.  и пусть
и пусть  - линейная функция. В таком случае статистика
- линейная функция. В таком случае статистика  является Н. о. для
является Н. о. для 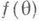 .
.
Следующий пример показывает, что имеются такие случаи, в к-рых Н. о. существуют и даже единственны, но при этом они могут оказаться бессмысленными.
Пример 4. Пусть X- случайная величина, подчиняющаяся геометрич. распределению, параметр успеха к-рого есть  , т. е. для любого натурального числа k
, т. е. для любого натурального числа k

Если  - Н. о. параметра
- Н. о. параметра  , то она должна удовлетворять уравнению несмещенности
, то она должна удовлетворять уравнению несмещенности 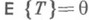 или, что то же самое, уравнению
или, что то же самое, уравнению

единственное решение к-рого есть

Очевидно, что статистика Тявляется хорошей только, если 9 очень близко к 1 либо к 0. в противном случае Тне несет никакой полезной информации о параметре 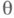 . Пример 5. Пусть случайная величина Xподчиняется биномиальному закону с параметрами пи
. Пример 5. Пусть случайная величина Xподчиняется биномиальному закону с параметрами пи  , т. е. для любого
, т. е. для любого 
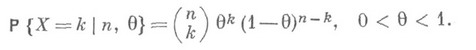
Известно, что наилучшей Н. о. (в смысле минимума квадратичного риска) параметра успеха 9 является статистика  Тем не менее, если 9 - иррациональное число, то
Тем не менее, если 9 - иррациональное число, то 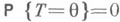 . Этот пример отражает одно общее свойство случайных величин, заключающееся в том, что случайная величина, вообще говоря, не обязана принимать значение, совпадающее с ее математич. ожиданием. И наконец, возможны случаи, когда Н. о. вообще не существуют. Так, если в условиях примера 5 в качестве оцениваемой функции выбрать
. Этот пример отражает одно общее свойство случайных величин, заключающееся в том, что случайная величина, вообще говоря, не обязана принимать значение, совпадающее с ее математич. ожиданием. И наконец, возможны случаи, когда Н. о. вообще не существуют. Так, если в условиях примера 5 в качестве оцениваемой функции выбрать
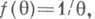 то (см. пример 6) не существует Н. о.
то (см. пример 6) не существует Н. о.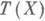 для
для  Приведенные примеры демонстрируют, что само по себе понятие Н. о., при всей своей естественности, не помогает экспериментатору избавиться от всех осложнений, к-рые могут ждать его при построении ста-тистич. оценок, так как Н. о. может оказаться как очень хорошей, так и совершенно бессмысленной, она может быть неединственной, а может вовсе не существовать. Кроме того, Н. о., как и всякая точечная оценка, обладает еще следующим недостатком: она дает лишь нек-рое приближенное значение для истинного значения оцениваемой величины, к-рое как было неизвестным до эксперимента, таковым и остается после его проведения. Вообще, в задаче построения точечных ста-тистич. оценок нет серьезных обоснований к тому, чтобы во всех случаях стремиться к получению Н. о., если не считать того, что при изучении Н. о. возникает простая и стройная теория. Так, напр., Рао- Крамера неравенство имеет простой вид для Н. о. Именно, если Т=Т (Х)- Н. о. для функции
Приведенные примеры демонстрируют, что само по себе понятие Н. о., при всей своей естественности, не помогает экспериментатору избавиться от всех осложнений, к-рые могут ждать его при построении ста-тистич. оценок, так как Н. о. может оказаться как очень хорошей, так и совершенно бессмысленной, она может быть неединственной, а может вовсе не существовать. Кроме того, Н. о., как и всякая точечная оценка, обладает еще следующим недостатком: она дает лишь нек-рое приближенное значение для истинного значения оцениваемой величины, к-рое как было неизвестным до эксперимента, таковым и остается после его проведения. Вообще, в задаче построения точечных ста-тистич. оценок нет серьезных обоснований к тому, чтобы во всех случаях стремиться к получению Н. о., если не считать того, что при изучении Н. о. возникает простая и стройная теория. Так, напр., Рао- Крамера неравенство имеет простой вид для Н. о. Именно, если Т=Т (Х)- Н. о. для функции 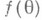 , то при довольно широких условиях регулярности семейства
, то при довольно широких условиях регулярности семейства  и функции
и функции  из неравенства Рао - Крамера следует,
из неравенства Рао - Крамера следует,
что
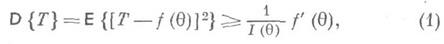
Где  - информационное количество Фишера. Таким образом, существует нижняя граница для дисперсий Н. о. функции
- информационное количество Фишера. Таким образом, существует нижняя граница для дисперсий Н. о. функции  , и этой границей служит
, и этой границей служит  . В частности, если
. В частности, если  , то из (1) следует, что
, то из (1) следует, что

Статистич. оценка, для к-рой в неравенстве Рао - Крамера достигается равенство, наз. эффективной. Так, статистика  рассмотренная в примере 5, является эффективной Н. о. параметра успеха
рассмотренная в примере 5, является эффективной Н. о. параметра успеха  биномиального закона, т. к.
биномиального закона, т. к.

т. е. 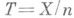 является наилучшей точечной оценкой параметра в смысле минимума квадратичного риска в классе всех Н. о.
является наилучшей точечной оценкой параметра в смысле минимума квадратичного риска в классе всех Н. о.
Естественно, что для экспериментатора представляет интерес тот случай, когда класс Н. о. достаточно богат, чтобы иметь возможность выбора наилучшей в каком-то смысле Н. о. В этой связи большую роль играет Рао- Блэкуэлла- Колмогорова теорема, позволяющая строить Н. о. с наименьшей дисперсией. Эта теорема утверждает, что если семейство {Ре } имеет достаточную статистику  , а
, а 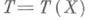 - произвольная Н. о. функции
- произвольная Н. о. функции  , то статистика
, то статистика 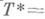
 , получающаяся в результате осреднения Тпри фиксированной достаточной статистике
, получающаяся в результате осреднения Тпри фиксированной достаточной статистике  , имеет риск, не превосходящий риска статистики Тотносительно произвольной выпуклой функции потерь при всех
, имеет риск, не превосходящий риска статистики Тотносительно произвольной выпуклой функции потерь при всех  . Если при этом семейство
. Если при этом семейство 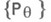 является полным, то статистика
является полным, то статистика  определяется единственным образом. То есть из теоремы Рао - Блэкуэлла - Колмогорова следует, что Н. о. нужно искать лишь в терминах достаточных статистик, если они существуют. Практич. ценность теоремы Рао - Блэкуэлла - Колмогорова заключается в том, что она дает рецепт построения наилучших Н. о., а именно: нужно построить произвольную Н. о. для
определяется единственным образом. То есть из теоремы Рао - Блэкуэлла - Колмогорова следует, что Н. о. нужно искать лишь в терминах достаточных статистик, если они существуют. Практич. ценность теоремы Рао - Блэкуэлла - Колмогорова заключается в том, что она дает рецепт построения наилучших Н. о., а именно: нужно построить произвольную Н. о. для  , а затем осреднить ее по достаточной статистике.
, а затем осреднить ее по достаточной статистике.
Пример 6. Пусть случайная величина Xимеет распределение Паскаля (отрицательное биномиальное распределение) с параметрами  т. е.
т. е.
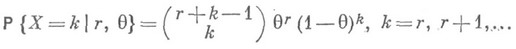
В этом случае статистика  является Н. о. параметра
является Н. о. параметра  . Так как статистика Твыражена в терминах достаточной статистики X, а система функций
. Так как статистика Твыражена в терминах достаточной статистики X, а система функций  является полной на отрезке [0, 1], то Тявляется единственной Н. о., а следовательно, наилучшей оценкой для 6.
является полной на отрезке [0, 1], то Тявляется единственной Н. о., а следовательно, наилучшей оценкой для 6.
Пример 7. Пусть X - случайная величина, подчиняющаяся биномиальному закону с параметрами пи 0. Производящая функция Q(z)этого биномиального закона выражается формулой

откуда следует, что для любого целого числа 


С другой стороны,

откуда следует, что
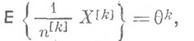
т. е. статистика

является Н. о. для  , причем в силу того, что
, причем в силу того, что  выражена в терминах достаточной статистики X, а также в силу полноты системы функций
выражена в терминах достаточной статистики X, а также в силу полноты системы функций  на отрезке [0, 1] следует, что
на отрезке [0, 1] следует, что  - единственная, а значит, и наилучшая Н. о. для
- единственная, а значит, и наилучшая Н. о. для 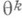 .
.
В связи с этим примером возникает следующий вопрос: какие функции  от параметра
от параметра 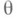 допускают несмещенное оценивание. А. Н. Колмогоров показал [1], что только для многочленов степени
допускают несмещенное оценивание. А. Н. Колмогоров показал [1], что только для многочленов степени  существуют Н. о. Так, если
существуют Н. о. Так, если
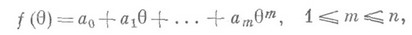
то из (2) следует, что статистика

является единственной Н. о. для  . Из этого результата, в частности, следует, что для функции
. Из этого результата, в частности, следует, что для функции  не существует Н. о.
не существует Н. о.
Пример 8. Пусть X- случайная величина, подчиняющаяся закону Пуассона с параметром  , т. е. для любого целого числа
, т. е. для любого целого числа 

В силу того, что  само наблюдение Xявляется Н. о. своего математич. ожидания 0. В свою очередь, напр., Н. о. функции
само наблюдение Xявляется Н. о. своего математич. ожидания 0. В свою очередь, напр., Н. о. функции 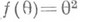 является
является 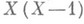
Вообще, статистика

является Н. о. функции 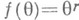 . Из этого факта, в частности, следует, что статистика
. Из этого факта, в частности, следует, что статистика

является Н. о. функции 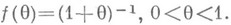 Вообще, если функция
Вообще, если функция 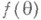 допускает несмещенное оценивание, то для нее должно выполняться уравнение несмещенности
допускает несмещенное оценивание, то для нее должно выполняться уравнение несмещенности  , к-рое равносильно следующему:
, к-рое равносильно следующему:

откуда получается, что Н. о. существует для любой функции 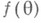 , допускающей разложение в степенной ряд в своей области определения
, допускающей разложение в степенной ряд в своей области определения 
Пример 9. Пусть независимые случайные величины 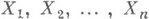 подчиняются одному и тому же закону Пуассона с параметром
подчиняются одному и тому же закону Пуассона с параметром  Производящая функция этого закона, выражающаяся формулой
Производящая функция этого закона, выражающаяся формулой

является целой аналитич. цией, и, следовательно, для нее существует единственная Н. о. Достаточной статистикой в этом случае является  к-рая подчиняется закону Пуассона с параметром nq. Если Т(Х)- Н. о. для
к-рая подчиняется закону Пуассона с параметром nq. Если Т(Х)- Н. о. для 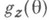 , то она должна удовлетворять уравнению несмещенности
, то она должна удовлетворять уравнению несмещенности
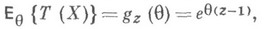
откуда следует, что

т. е. Н. о. для производящей функции закона Пуассона является производящая функция биномиального закона с параметрами Xи 1/n.
Примеры 6-9 демонстрируют, что в нек-рых случаях, довольно часто встречающихся на практике, именно благодаря понятию Н. о. задача построения наилучших оценок оказывается легко разрешимой, если ограничиться классом Н. о. А. Н. Колмогоров [1] рассмотрел вопрос построения Н. о., в частности задачу построения Н. о. функции распределения нормального закона, параметры к-рого неизвестны. Э. Леману (Е. Lehmann) принадлежит более общее определение Н. о. Согласно определению Э. Лемана (см. [2]) статистич. оценка Т=Т(X)параметра  наз. несмещенной относительно функции потерь
наз. несмещенной относительно функции потерь 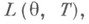 если
если

Имеется модификация этого определения (см. [3]). Ю. В. Линником и его учениками (см. [4]) была установлена независимость наилучшей Н. о. от функции потерь при довольно широких предположениях.
Лит.:[1] Колмогоров А. Н., "Изв. АН СССР. Сер. матем.", 1950, т. 14, №4, с. 303-28; [2] Леман Э., Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979; [3] Клебанов Л. Б., "Теория вероятн. и ее применения", 1976, т. 21, № 3, с. 584-98; [4] Клебанов Л. Б., Пинпик Ю. В., Рухин А. Л., "Докл. АН СССР", 1971, т. 200, № 5, с. 1024-25; [5] 3акс Ш., Теория статистических выводов, пер. с англ., М., 1975.
М. С. Никулин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.