1)С. р. по одному комплексному переменному z - функциональный ряд вида

где a - центр ряда, bk - его коэффициенты, bk(z-a)k - члены ряда. Существует число r,  называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши - Адамара
называемое радиусом сходимости С. р. (1) и определяемое по формуле Коши - Адамара

такое, что при |z-а|<r ряд (1) абсолютно сходится, а при |z- а|>r - расходится (теорема Коши - Адамара). В связи с этим круг 
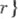 на плоскости
на плоскости 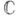 комплексного переменного z наз. кругом сходимости С. р. (см. рис. 1). В случае r=0 круг сходимости вырождается в единственную точку z=a, напр. для С. р.
комплексного переменного z наз. кругом сходимости С. р. (см. рис. 1). В случае r=0 круг сходимости вырождается в единственную точку z=a, напр. для С. р.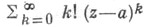 (этот случай интереса не представляет, и всюду в дальнейшем предполагается, что r>0). В случае
(этот случай интереса не представляет, и всюду в дальнейшем предполагается, что r>0). В случае  круг сходимости совпадает со всей плоскостью
круг сходимости совпадает со всей плоскостью  напр. для С. р.
напр. для С. р. Множество сходимости, т. е. совокупность всех точек сходимости С. р. (1), в случае
Множество сходимости, т. е. совокупность всех точек сходимости С. р. (1), в случае  кроме точек круга сходимости D, может включать все или нек-рые точки, или ни одной точки окружности сходимости
кроме точек круга сходимости D, может включать все или нек-рые точки, или ни одной точки окружности сходимости 
 Круг сходимости в этом случае есть внутренность множества точек абсолютной сходимости С. р.
Круг сходимости в этом случае есть внутренность множества точек абсолютной сходимости С. р.

Внутри круга D, т. е. на любом компакте  С. р. (1) сходится абсолютно и равномерно. Таким образом, сумма ряда s(z) определена и является регулярной аналитич. цией по крайней мере в круге D. При этом на окружности Sона имеет по меньшей мере одну особую точку, аналитич. родолжение в к-рую суммы s(z) невозможно. Существуют С. р., имеющие на Sв точности одну особую точку, равно как н С. р., у к-рых вся окружность Sсостоит из особых точек.
С. р. (1) сходится абсолютно и равномерно. Таким образом, сумма ряда s(z) определена и является регулярной аналитич. цией по крайней мере в круге D. При этом на окружности Sона имеет по меньшей мере одну особую точку, аналитич. родолжение в к-рую суммы s(z) невозможно. Существуют С. р., имеющие на Sв точности одну особую точку, равно как н С. р., у к-рых вся окружность Sсостоит из особых точек.
В случае  ряд (1) либо обрывается, т. е. представляет собой многочлен
ряд (1) либо обрывается, т. е. представляет собой многочлен

либо его сумма s(z) есть целая трансцендентная функция, регулярная во всей плоскости  и имеющая в бесконечности существенно особую точку.
и имеющая в бесконечности существенно особую точку.
Обратно, само понятие аналитичности функции f(z) в точке асостоит в том, что f(z) в нек-рой окрестности аразлагается в С. р.

к-рый является для f(z) рядом Тейлора, т. е. его коэффициенты определяются формулами

В связи с этим важно свойство единственности С. р.: если сумма s(z)ряда (1) обращается в нуль на бесконечном множестве  имеющем предельную точку внутри D, то
имеющем предельную точку внутри D, то  и все bk=-0, k=0, 1, ... В частности, если s(z)=0 в окрестности нек-рой точки
и все bk=-0, k=0, 1, ... В частности, если s(z)=0 в окрестности нек-рой точки  то
то  и все bk=0. Таким образом, всякий С. р. есть ряд Тейлора для своей суммы. Пусть наряду с С. р. (1) имеется другой С. р.
и все bk=0. Таким образом, всякий С. р. есть ряд Тейлора для своей суммы. Пусть наряду с С. р. (1) имеется другой С. р.

с тем же центром аи радиусом сходимости r1>0. Тогда по крайней мере в круге  где
где  имеют смысл сложение, вычитание и умножение С. р. (1) и (3) по формулам:
имеют смысл сложение, вычитание и умножение С. р. (1) и (3) по формулам:

Законы коммутативности, ассоциативности и дистрибутивности справедливы, причем вычитание есть действие, обратное сложению. Таким образом, множество С. р. с положительными радиусами сходимости и фиксированным центром есть кольцо над полем С. Если  то возможно и деление С. р.:
то возможно и деление С. р.:

причем коэффициенты dk однозначно определяются из бесконечной системы уравнений

При  r>0 и r1>0 радиус сходимости ряда (5) также положительный.
r>0 и r1>0 радиус сходимости ряда (5) также положительный.
Пусть для простоты в (1) и (3)  Тогда сложная функция
Тогда сложная функция 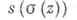 будет регулярной в окрестности начала координат, и процедура разложения ее в С. р. носит название подстановки ряда в ряд:
будет регулярной в окрестности начала координат, и процедура разложения ее в С. р. носит название подстановки ряда в ряд:
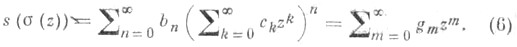
Коэффициент gm в(6) получается как сумма одноименных коэффициентов в разложениях каждой из функций  а эти последние разложения получаются путем n-кратного умножения ряда для
а эти последние разложения получаются путем n-кратного умножения ряда для  самого на себя. Ряд (6) заведомо сходится при
самого на себя. Ряд (6) заведомо сходится при  где
где 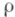 таково, что
таково, что  Пусть опять
Пусть опять  и, кроме того,
и, кроме того, Задача построения ряда для обратной функции
Задача построения ряда для обратной функции  к-рая при указанных условиях регулярна в окрестности начала, наз. обращением ряда (3). Ее решением является ряд Лагранжа:
к-рая при указанных условиях регулярна в окрестности начала, наз. обращением ряда (3). Ее решением является ряд Лагранжа:
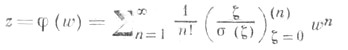
(о более общей задаче обращения см. в ст. Бюрмана- Лагранжа ряд).
Если С. р. (1) сходится в нек-рой точке  то он абсолютно сходится для всех z таких, что |z-а|< |z0 -а| ,- в этом состоит первая теорема Абеля. Эта теорема также позволяет установить вид области сходимости С. р. Более тонкий результат представляет собой вторая теорема Aбeля: если С. р. (1) сходится в точке
то он абсолютно сходится для всех z таких, что |z-а|< |z0 -а| ,- в этом состоит первая теорема Абеля. Эта теорема также позволяет установить вид области сходимости С. р. Более тонкий результат представляет собой вторая теорема Aбeля: если С. р. (1) сходится в точке  на окружности сходимости S, то
на окружности сходимости S, то

т. е. сумма ряда s(z) в точке  имеет радиальное граничное значение s(z0 )и, следовательно, непрерывна вдоль радиуса
имеет радиальное граничное значение s(z0 )и, следовательно, непрерывна вдоль радиуса  более того, s(z)имеет и угловое граничное значение s(z0). Эту теорему (1827) можно считать первым крупным результатом в направлении исследования граничных свойств С. р. Обращение второй теоремы Абеля без дополнительных ограничений на коэффициенты С. р. невозможно. Однако, если предположить, напр., что bk=0(1/k )и существует предел
более того, s(z)имеет и угловое граничное значение s(z0). Эту теорему (1827) можно считать первым крупным результатом в направлении исследования граничных свойств С. р. Обращение второй теоремы Абеля без дополнительных ограничений на коэффициенты С. р. невозможно. Однако, если предположить, напр., что bk=0(1/k )и существует предел  то ряд
то ряд  сходится к сумме s0. Такого рода частичные обращения второй теоремы Абеля получили название тауберовых теорем.
сходится к сумме s0. Такого рода частичные обращения второй теоремы Абеля получили название тауберовых теорем.
Другие результаты о граничных свойствах С. р. и, в частности, о расположении особых точек С. р. см. в статьях Адамара теорема, Аналитическое продолжение, Граничные свойства аналитических функций, Фату теорема (см. также [3] - [5]).
2) С. р. по многим комплексным переменным z=(z1, . . .. zn), n>1, или кратный С. р.- функциональный ряд вида

где 
 - центр ряда, точка комплексного пространства
- центр ряда, точка комплексного пространства  Областью сходимости DС. р. (7) наз. внутренность множества точек абсолютной сходимости, но при п>1 она не имеет столь простого вида, как при n=1. Область Dпространства
Областью сходимости DС. р. (7) наз. внутренность множества точек абсолютной сходимости, но при п>1 она не имеет столь простого вида, как при n=1. Область Dпространства  тогда и только тогда является областью сходимости нек-рого С. р. (7), когда D - логарифмически выпуклая полная кратно круговая область пространства
тогда и только тогда является областью сходимости нек-рого С. р. (7), когда D - логарифмически выпуклая полная кратно круговая область пространства  Если нек-рая точка
Если нек-рая точка  то замыкание
то замыкание  поликруга
поликруга 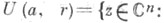
 где
где  r=(r1, . . ., rn), также принадлежит Dи ряд (7) сходится в
r=(r1, . . ., rn), также принадлежит Dи ряд (7) сходится в  абсолютно и равномерно (аналог первой теоремы Абеля). Поликруг U(a, r), r=(r1, . . ., rn), наз. поликругом сходимости С. р. (7), если
абсолютно и равномерно (аналог первой теоремы Абеля). Поликруг U(a, r), r=(r1, . . ., rn), наз. поликругом сходимости С. р. (7), если  но в любом несколько большем поликруге
но в любом несколько большем поликруге  где
где  и по крайней мере одно неравенство строгое, имеются точки, в к-рых ряд (7) расходится. Радиусы
и по крайней мере одно неравенство строгое, имеются точки, в к-рых ряд (7) расходится. Радиусы  поликруга сходимости наз. сопряженными радиусами сходимости С. р. (7), они удовлетворяют соотношению, являющемуся аналогом формулы Коши - Адамара:
поликруга сходимости наз. сопряженными радиусами сходимости С. р. (7), они удовлетворяют соотношению, являющемуся аналогом формулы Коши - Адамара:

где 

Область сходимости Dисчерпывается поликругами сходимости. Напр., для ряда  поликруги сходимости имеют вид
поликруги сходимости имеют вид
 а область сходимости
а область сходимости  (на рис. 2 она изображена на абсолютной четверть-плоскости).
(на рис. 2 она изображена на абсолютной четверть-плоскости).

Свойство единственности С. р. сохраняется в том смысле, что если s(z) = 0 в нек-рой окрестности точки z0 в 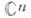 (достаточно даже в
(достаточно даже в  т. е. на множестве
т. е. на множестве 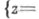
 то
то  и все bk=0.
и все bk=0.
Действия с кратными С. р. производятся в основном по тем же правилам, что и в случае n=1. Другие свойства кратных С. р. см., напр., [8], [9].
3) С. р. по действительным переменным х= (x1, . . ., xn), 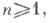 - функциональный ряд вида
- функциональный ряд вида

где использованы сокращенные обозначения, как и в (7),  - центр ряда. Если ряд (8) абсолютно сходится в нек-ром параллелепипеде
- центр ряда. Если ряд (8) абсолютно сходится в нек-ром параллелепипеде 
 то он абсолютно сходится и в поликруге
то он абсолютно сходится и в поликруге  r=(r1,. . ., rn). При этом сумма ряда s(x), будучи аналитич. цией действительных переменных x= (x1, . . ., х п )в П, аналитически продолжается в виде С. р.
r=(r1,. . ., rn). При этом сумма ряда s(x), будучи аналитич. цией действительных переменных x= (x1, . . ., х п )в П, аналитически продолжается в виде С. р.
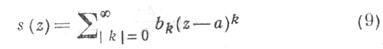
до аналитич. ции s(z) комплексных переменных z=x+iy=(z1=x1+iyl, . . ., zn=-xn+iyn )в U( а, r). Если D- область сходимости С. р. (9) в пространстве  комплексных переменных z=x+iy, то сужение
комплексных переменных z=x+iy, то сужение  области Dна пространство
области Dна пространство  действительных переменных x=(x1,. . ., х п) является областью сходимости С. р. (8),
действительных переменных x=(x1,. . ., х п) является областью сходимости С. р. (8),  В частности, при n=1 область Dявляется кругом сходимости, а его сужением
В частности, при n=1 область Dявляется кругом сходимости, а его сужением  является интервал сходи мости на числовой оси
является интервал сходи мости на числовой оси 
 где r - радиус сходимости.
где r - радиус сходимости.
Лит.:[1] Бицадзе А. В., Основы теории аналитических функций комплексного переменного, 2 изд., М., 1972; [2] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [3] Титчмарш Е., Теория функций, пер. е англ., М.-Л., 1951; [4] Бибербах Л., Аналитическое продолжение, пер. с нем., М., 1967: [5] Landau E., Darstellung und Begrundung einiger neuerer Ergebnisse der Funktionentheorie, 2 Aufl., В., 1929; [6] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1984; [7] Шабат Б. В., Введение в комплексный анализ, 2 изд., ч. 1-2, М., 1976; [8] Бохнер С., Мартин У. Т., Функции многих комплексных переменных, пер. с англ., М., 1951; [9] Янушаускас А. И., Двойные ряды, Новосиб., 1980.
Е. Д. Соломенцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.