Akademik

в теории вероятностей - одно из важнейших понятий этой теории. Иногда используют термины статистическая независимость, стохастическая независимость. Предположение о Н. рассматриваемых событий, испытаний и случайных величин было обычной предпосылкой в задачах, к-рые рассматривались в математической вероятностей теории со времени ее возникновения.

Для двух случайных событий понятие Н. вводится следующим образом. Пусть - два случайных события, - их вероятности. Условную вероятность события Впри условии осуществления события Аопределяют формулой

где - вероятность совместного осуществления событий Аи В. События Аи Вназ. независимыми, если

При это равносильно соотношению

Смысл данного определения Н. можно пояснить следующим образом. Предполагая, что производится большое число Nиспытаний, и переходя в (2) от вероятностей к частотам, можно заключить, что между частотой события Вво всех Nиспытаниях и частотой его появления в тех испытаниях, в к-рых наступает А, должно иметь место приближенное равенство. Н. событий указывает таким образом либо на отсутствие связи между наступлением одного из этих событий и наступлением другого, либо на несущественный характер этой связи. Так, событие, заключающееся в том, что наудачу выбранное лицо имеет фамилию, начинающуюся, напр., с буквы "А", и событие, заключающееся в том, что этому лицу достанется выигрыш в очередном тираже лотереи,- независимы.

Определение Н. пслучайных событий может быть дано в нескольких равносильных вариантах. Согласно одному из них эти события наз. независимыми, если для любого <:, и для произвольных попарно различных натуральных чисел вероятность совместного осуществления событий равна произведению их вероятностей

Отсюда, как и ранее, можно вывести, что условная вероятность каждого из рассматриваемых событий при условии, что какие-либо из остальных наступили, равна его "безусловной" вероятности.

Иногда наряду с Н. (взаимной Н.) событий рассматривают так наз. попарную Н., означающую, что любые два из этих событий и независимы. Н. событий влечет их попарную Н', а обратное, вообще говоря, неверно.

В период, предшествовавший аксиоматич. построению теории вероятностей, содержание понятия Н. не воспринималось достаточно отчетливо. "Понятие о независимых событиях можно считать вполне ясным в известных теоретических вопросах; в других же вопросах это понятие, конечно, может совершенно затемняться вместе с затемнением основного понятия о вероятности",- писал А. А. Марков (см. [1] с. 24).

В рамках аксиоматич. подхода понятие Н. наиболее естественно вводится следующим образом. Пусть (, ) - какое-либо вероятностное пространство, где 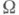- множество элементарных событий,,- -алгебра событий,- определенная на 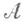вероятностная мера. Сначала определяют Н. классов событий (здесь будут рассмотрены только классы , являющиеся -подалгебрами -алгебры ,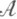). Классы наз. независимыми (относительно Р), если любые события независимы в смысле равенства (3); классы 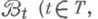где - произвольное множество индексов) наз. независимыми, если при любом целом и любых попарно различных классы независимы. Н. событий равносильна Н. классов

Для испытаний Н.- это Н. порождаемых ими s-алгебр. Для случайных величин , Н. определяют как Н. -подалгебр , где - прообраз относительно отображения s-алгебры борелевских множеств на числовой прямой. Н. случайных событий равносильна Н. их индикаторов т. е. случайных величин, определяемых формулами

и

Для Н. случайных величин необходимы и достаточны следующие условия.

1) Для любых действительных чисел функция распределения

равна произведению соответствующих функций распределения:

2) При наличии плотностей

плотность для почти всех по лебеговой мере в значений равна произведению

соответствующих плотностей.

3) Характеристич. функция

для всех действительных чисел равна

произведению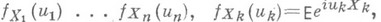

соответствующих характеристич. функций.

На гипотезе Н. тех или иных событий и случайных величин основаны важнейшие схемы теории вероятностей: последовательности независимых случайных величин (см., напр., Бернулли блуждание, Больших чисел закон, Предельные теоремы теории вероятностей), случайные процессы с независимыми приращениями (см., напр., Винеровский процесс, Случайный процесс )и т. д. (см. также Нуль-единица закон).

Общие замечания к понятию независимости.

1) Независимость функций от независимых случайных величин. Из данной Н. случайных величин можно вывести довольно очевидные (и вполне соответствующие интуитивно ожидаемым от понятия Н.) следствия; напр., функции от и от 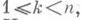будут независимыми случайными величинами. Н. другого типа функций может иметь место только при специальных дополнительных предположениях и может служить для характеризации определенных классов распределений. Напр., если независимы, одинаково распределены и имеют нормальное распределение, то функции

(статистич. оценки математич. ожидания и дисперсий соответственно) являются независимыми случайными величинами. Верно и обратное утверждение: из Н. функций (4) и (5) вытекает нормальность распределений . Точно так же, если известно, что две линейные формы

являются независимыми случайными величинами и ни один из коэффициентов и не равен нулю, то все имеют нормальное распределение (из подобного рода теорем может быть при минимальных допущениях выведен, напр., закон Максвелла для распределения скоростей молекул). Приведенные утверждения служат примерами т. н. характеризационных теорем, наиболее полно изученных Ю. В. Линником и его школой.

2) Существование независимых случайных величин на заданном вероятностном пространстве. Если множество элементарных событий состоит из трех элементов, каждому из к-рых приписана вероятность, равная 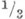, то на не существует независимых случайных величин, отличных от констант. Если в качестве вероятностного пространства взят отрезок [0, 1] с мерой Лебега т, то для любой последовательности функций распределения найдутся определенные на [0, 1] измеримые функции , являющиеся по отношению к тнезависимыми случайными величинами и такие, что

Простейшим примером такого рода статистически независимых функций на [0, 1] служат знаки двоичного разложения или связанные с ними функции Радемахера

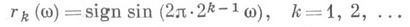
Следует отметить, что существование какого-нибудь вероятностного пространства, на к-ром определены независимые случайные величины с заданными распределениями, вытекает из теоремы Колмогорова о вероятностях в бесконечномерных пространствах (см. [3] гл. III, 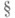4).

3) Независимые случайные величины как источник других схем. Пусть - последовательность независимых случайных величин и - (борелев-ская) функция двух переменных. Полагая

получают последовательность случайных величин, образующих Маркова цепь. Подобным же образом можно получать марковские процессы, напр, из винеровского процесса при помощи стохастических дифференциальных уравнений. Из гауссовскпх случайных мер с независимыми значениями можно, используя преобразование Фурье, построить гауссовские стационарные случайные процессы и т. д.

4) Слабая зависимость. Асимптотич. законы теории вероятностей, установленные для последовательностей независимых случайных величин, обычно могут быть распространены и на последовательности т. н. слабо зависимых величин, т. е. на последовательности где надлежащим образом измеренная зависимость между "удаленными" друг от друга отрезками последовательности "мала" (в простейших случаях это могут быть последовательности m-зависпмых величин, где и при независимы, или последовательности величин, образующих Маркова цепь эргодическую, и т. п.). Один из основных приемов доказательства соответствующих теорем - сведение рассматриваемого случая к случаю Н.

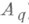5) Независимость в теории чисел. Пусть и - два взаимно простых натуральных числа. Пусть N- натуральное число, и пусть наудачу выбирают одно из чисел от 1 до N (вероятность для каждого считают равной ). Пусть (соответственно ) событие, состоящее в том, что выбранное число делится нацело на р(соответственно q). Тогда

и при события и становятся "почти независимыми". Значительно более глубокий факт, состоящий в том, что при можно выбрать так, что события (A_j есть j-е простое число) в совокупности "почти независимы", служит основой для исследования распределения значений арифметич. функций, см. Чисел теория;вероятностные методы. Имеются и другие разделы теории чисел, где идея Н. явно или неявно присутствует.

6) О проверке гипотезы Н. по результатам наблюдений см. Статистических гипотез проверка.

Лит.:[1] Марков А. А., Исчисление вероятностей, 4 изд., М., 1924; [2] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974; [3] его же, Теория вероятностей, в кн.: Математика, ее содержание, методы и значение, М., 1956; [4] Кац М., Статистическая независимость в теории вероятностей, анализе и теории чисел, пер. с англ., М., 1963; [5] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., М.. 1967.

Ю. В. Прохоров.