Akademik

в банаховом пространстве - раздел функционального анализа, в к-ром исследуется поведение на действительной оси J или на положительной (отрицательной) полуоси J⁺ (J^-) решений эволюционных уравнений в банаховом пространстве. Рассматриваются уравнения

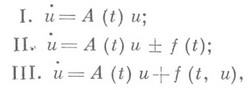
где u(t)- искомая, a f(t)- заданная функция со значениями в комплексном банаховом пространстве Е, A(t)- линейный оператор, f(t, и)- нелинейный оператор в Е. Под производной ипонимается предел по норме пространства Е отношения при

Для дифференциального уравнения I имеется равномерная устойчивость (р. у.), если существует константа Мтакая, что для любого решения и экспоненциальная устойчивость (э. у.), если для всех решений 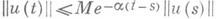при нек-рых Ми a>0.

Для уравнения I с постоянным ограниченным оператором A(t)=A решение задачи Коши (u(s)задано) имеет вид u(t) = e^(t-s)Au(s). Справедлива оценка 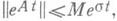где а- число, большее всех действительных частей точек спектра оператора А. Таким образом, для э. у. необходимо и достаточно, чтобы спектр А лежал внутри левой полуплоскости. В гильбертовом пространстве это имеет место тогда и только тогда, когда существует положительно определенная форма (Wx,y), для к-рой на любом решении уравнения (теорема Ляпунова). Если спектр Арасположен по обе стороны от мнимой оси и не пересекается с ней, то пространство Еразлагается в прямую сумму инвариантных относительно Аподпространств Е ₊ и Е _-, причем все решения в E₊(E_-) экспоненциально возрастают (убывают) при В этом случае для уравнения имеет место экспоненциальная дихотомия (э. д.).

Если оператор Анеограничен, замкнут и имеет плотную в Еобласть определения, то задача Коши с u(0)= u₀, вообще говоря, не является корректной. Существование и свойства ее решений не определяются только расположением спектра оператора А, необходимо еще определенное поведение его резольвенты (А-lI)^-1. Употребительными условиями, обеспечивающими равномерную корректность задачи Коши на J⁺ , являются неравенства

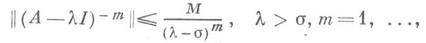
для выполнения к-рых достаточно условие Xилле - Иосиды

или неравенство

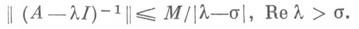
При выполнении их решение задачи Коши имеет вид u(t)=T(t-s)u(s), где T(t)- сильно непрерывная при полугруппа операторов, причем

Для р. у. (э. у.) достаточно, чтобы было s=0 (s<0). Если оператор Апорождает сильно непрерывную полугруппу в гильбертовом пространстве, то для него справедлива достаточная часть теоремы Ляпунова, а если - группу, то - и необходимая. В гильбертовом пространстве э. у. эквивалентна L₂ -устойчивости, т. е. тому, что для всех решений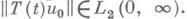

Важным для приложений свойством решений u(t)является почти периодичность (п. п.) или слабая почти периодичность (то есть п. п. скалярных функций 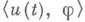для всех ).

Все значения п. п. решения лежат в компактном множестве - решение компактно. Из компактности и слабой п. п. следует п. п. Для уравнения и=А (и)вопрос о п. п. решений связан со структурой пересечения спектра Ас мнимой осью. Если А- производящий оператор ограниченной сильно непрерывной полугруппы и указанное пересечение счетно, то для п. п. определенного на всей оси и ограниченного решения необходимо и достаточно, чтобы существовал предел 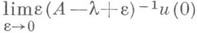в каждой предельной точке спектра %на мнимой оси. При этом всякое равномерно непрерывное решение слабо п. п.; оно п. п., если оно слабо компактно, или если Ене содержит подпространств, изоморфных пространству С ₀ последовательностей, стремящихся к нулю с нормой max. Если А- производящий оператор сильно непрерывной полугруппы T(t), к-рая обладает тем свойством, что функции ||Т*(t)j|| ограничены на J⁺ для плотного в Е* множества функционалов ф, то из компактности решения следует п. п.

Для уравнения I с ограниченным и непрерывным по tоператором A(t)решения задачи Коши определены на всей оси, и с помощью эволюционного оператора U(t, s )записываются в виде u(t)= U(t, s) и(s). Свойство р. у. эквивалентно тому, что 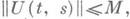свойство э. у.- тому, что 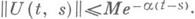Если оператор А(t) интегрально ограничен, т. е.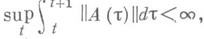то генеральный показатель конечен. Если х<0, то имеет место э. у. Для уравнений с постоянным или периодич. оператором A(t)справедлива формула В общем случае она неверна. Генеральный показатель не изменяется, если оператор A(t)возмущается слагаемым B(t), для к-рого при 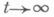или для к-рого сходится на бесконечности интеграл Величина генерального показателя зависит от поведения A(t)на бесконечности. Если существует предел 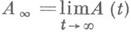и спектр А лежит внутри левой полуплоскости, то х<0. Если операторы А(t), 0 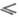t< образуют компактное множество в пространстве ограниченных операторов, спектры всех предельных операторов лежат в полуплоскости и оператор-функция A(t)мало осциллирует, напр., имеет вид В(et). при достаточно малом e или при достаточно больших tудовлетворяет условию Липшица с достаточно малым e, то x<0.

В гильбертовом пространстве условие х <0 эквивалентно существованию эрмитовой формы (W(t)x, у )такой, что 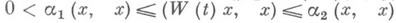и

для любого решения u(t).

Если оператор A(t)периодичен с периодом со, A(t+ w) = A(t), то оператор U(t, s )обладает свойством U(t+w, 0)=U(t,0)U(w, 0). Оператор U(w)=U(w, 0) наз. оператором монодромии уравнения I. Его спектральный радиус r_u(w) связан с генеральным показателем х формулой Уравнение имеет периодич. решения тогда и только тогда, когда 1 является собственным числом U(w). Если оператор U(w). обладает логарифмом, то справедливо представление Флоке U(t, 0) = Q(t)e^tГ, где Q(t)периодичен с периодом со, а 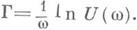В частности, представление Флоке имеет место, если спектр U(w) не окружает нуля, для чего достаточно, чтобы

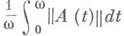было меньше нек-рой константы, зависящей от геометрии сферы в Еи не меньшей ln4. Для гильбертова пространства эта константа равна p. Представление Флоке сводит вопрос о поведении решений уравнения с периодич. оператором к такому же вопросу для уравнения u=Гvс постоянным оператором Г.

Для уравнения I имеет место экспоненциальная дихотомия(э. д.), если для нек-рого sпространство Еразлагается в прямую сумму подпространств E₊(s)и E_-(s)так, что

пр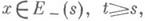и и

при При этом предполагается, что подпространства U(t,s)E₊(s)и U(t,s)E_-(s)в определенном смысле не должны сближаться. В случае конечности генерального показателя последнее условие выполняется автоматически. Для того чтобы для уравнения с периодич. A(t)имела место э. д., необходимо и достаточно, чтобы спектр оператора монодромии располагался вне и внутри единичного круга, но не пересекался с единичной окружностью.

Для уравнения I с неограниченным оператором A(t)с не зависящей от tобластью определения, удовлетворяющим условиям корректности задачи Коши (см. выше) при каждом t, при дополнительных условиях гладкости доказано существование эволюционного оператора U(t, s), определенного и сильно непрерывного по t и s при 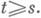Это позволяет перенести на этот случай ряд понятий и результатов, описанных выше. Однако здесь встречаются трудности. Так, представление Флоке получено лишь для уравнений в гильбертовом пространстве, когда A(t) = A+ B (t), где А- отрицательно определенный самосопряженный оператор, а В(t)- ограниченный периодич. оператор, удовлетворяющий нек-рым дополнительным условиям.

Пусть A(t)периодичен, и задача Коши для уравнения I равномерно корректна. Если пересечение спектра оператора монодромии U(w) с единичной окружностью счетно, то каждое ограниченное равномерно непрерывное на J решение слабо п. п. Оно - п. п. в случае слабой компактности или если Ене содержит с ₀. В рефлексивном пространстве Есуществует разложение в прямую сумму Е ₁+Е₂ такое, что Е ₁ и Е ₂ инвариантны относительно U(w), и все решения, начинающиеся в E₁ являются п. п., а начинающиеся в Е ₂- в определенном смысле убывают: при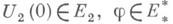

Для решения неоднородного уравнения II справедлива формула

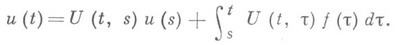
Для уравнения с ограниченным оператором это равенство эквивалентно дифференциальному уравнению. В случае неограниченного оператора, это, вообще говоря, не так, но тогда это равенство принимается за определение (обобщенного) решения. Основной задачей для уравнения II является исследование свойств решений при заданных свойствах правой части. Эти свойства обычно описываются как принадлежность функции какому-либо банахову пространству функций на J или J⁺ со значениями в Е. Если каждой непрерывной ограниченной функции 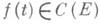отвечает хотя бы одно ограниченное решение, то оператор 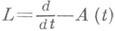наз. слабо регулярным. Если каждой 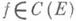отвечает единственное решение 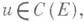то Lназ. регулярным. Для ограниченного постоянного Аиз слабой регулярности следует регулярность. Для неограниченного Аили ограниченного периодического A(t)этот факт уже может быть неверным даже в гильбертовом пространстве. Если генеральный показатель уравнения и = А(t)uконечен, то э. д. для этого уравнения эквивалентна регулярности оператора Lна J. Для того чтобы э. д. имела место на полуоси J⁺ , необходимо и достаточно, чтобы оператор Lна J⁺ был слабо регулярным и чтобы множество тех начальных значений и(0), к-рым отвечают ограниченные решения уравнений I, было дополняемым подпространством Е. Если для всех решений уравнения II выполнено неравенство а для решений формально сопряженного уравнения 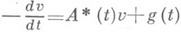- неравенство 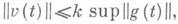то операторы Lи 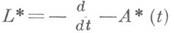регулярны. Неизвестно (1978), сохранится ли регулярность, если справа в первом неравенстве стоит 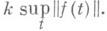Для регулярности Lи L* обе априорныеоценки необходимы.

Если A(t)периодичен, то для существования периодич. решения при всякой периодич. f(t)необходимо и достаточно, чтобы отображение I-U(w)было сюръективным, а для того чтобы такое решение было единственным, необходимо и достаточно, чтобы оператор I-U(w) был обратимым.

Проверка регулярности при известных условиях может быть сведена к проверке регулярности операторов с постоянными коэффициентами. В случае сильной осцилляции А(t) (напр., A(t)=B(wt). с большим w) при условии существования среднего 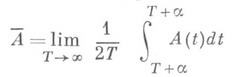равномерно по 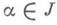оператор А(t) регулярен тогда и только тогда, когда регулярен оператор

Для почти периодических решений специфика бесконечномерного пространства сказывается уже на обобщении известной теоремы Боля-Бора о п. п. ограниченного интеграла от п. п. функции, то есть о п. п. ограниченного решения простейшего. уравнения u=f(t). Если неопределенный интеграл от п. п. функции со значениями в Еограничен и Ене содержит с ₀, то он является п. п. В пространстве с ₀ теорема Боля-Бора неверна. Если A(t)периодичен, f(t)- почти периодична и пересечение спектра оператора монодромии U(w) с единичной окружностью счетно, то справедливы те же выводы о п. п. решения, к-рые сформулированы выше для однородного уравнения. Если A(t)почти периодичен (как функция со значениями в пространстве ограниченных операторов в E),тодля того чтобы при всякой п. п. f(t)существовало единственное п. п. решение, необходимо и достаточно, чтобы оператор Lбыл регулярным. Если уравнение II имеет (слабо) компактное при t>0 решение, и нетривиальные (слабо) компактные решения однородного уравнения и=А(t)uобладают тем свойством, что то уравнение II имеет (слабо) п. п. решение.

При качественном исследовании нелинейного уравнения 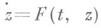обычно заранее предполагаются выполненными условия, обеспечивающие существование решений на J или на J⁺ , что налагает существенные ограничения на вид нелинейности F(t,z). Решение z₀(t)на J⁺ наз. равномерно устойчивым (р. у.), если для всякого е существует d такое, что для всякого другого решения z(t) из неравенства ||z(s)-z₀(s)||d, следует, что z(t)определено при и ||z(t) -z₀ (t)||e. Решение наз. асимптотически устойчивым (а. у.), если оно р. у. п при нек-ром d. из неравенства 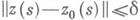следует, что 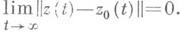Если в уравнении сделать замену u=z-z₀(t), то после линеаризации (если она возможна) оно принимает вид III, где A(t)=F'_z(t, z₀(t)), а нелинейность обладает тем свойством, что f(t, 0)=0. Таким образом, задача о р. у. или а. у. решения z₀(t)сводится к задаче о р. у. или а. у. нулевого решения уравнения

III. Уравнение при этом наз. уравнением в вариациях для исходного уравнения относительно решения z₀(t).

Если нелинейная часть f(t, и )достаточно мала, то свойства решении определяются свойствами решений уравнения в вариациях. Если генеральный показатель уравнения в вариациях отрицателен, и выполнено неравенство 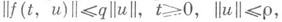то при достаточно малом qнулевое решение уравнения III будет а. у. Если A(t)=A и спектр Ане пересекается с мнимой осью и имеет точки в правой полуплоскости, то при достаточно малом qнулевое решение неустойчиво. Если выполнено неравенство

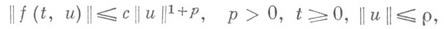
то требование отсутствия точек спектра на мнимой оси можно отбросить.

Если для уравнения в вариациях имеет место э. д. на J, то для каждого р>0 существуют такие Ми с, зависящие только от A(t)и р, что из неравенств

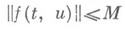
и

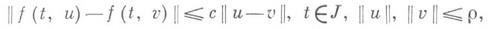
следует существование в нек-рой окрестности нуля многообразий М ₊ и M_-, пересекающихся в одной точке u₀, таких, что решение u₀(t), начинающееся в u₀, ограничено на всей оси, и решения, начинающиеся на M_- ( М ₊), экспоненциально приближаются при 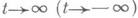к u₀(t)и удаляются от него при t, неограниченно изменяющемся в противоположном направлении. При этом М ₊ (М _-) гомеоморфны окрестностям пространств E₊ (0) и E_- (0), участвующих в определении э. д. Если в предыдущих условиях и f(t, и)п. п. по tпри каждом ис то решение u₀(t)п. п. Пусть автономное уравнение z=F(z)имеет w-периодич. решение z₀ (t), тогда уравнение в вариациях 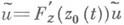имеет одно периодич. решение и, следовательно, его оператор монодромии U(w). имеет 1 собственным числом. Если это число простое и остальной спектр U(w) лежит внутри единичного круга и не окружает нуля, то существуют такие числа m>0, t₀ и N, что для всех других решений исходного уравнения ||z(t-z₀)- -z(i)||Ne^-mt. Указанное свойство наз. асимптотической орбитальной устойчивостью периодич. решения. Имеются исследования и других устойчивых инвариантных многообразий для нелинейных уравнений.

Уравнения вида III с неограниченным оператором A(t)в приложениях соответствуют квазилинейным уравнениям параболич. и гиперболич. типа. Развита теория "истинно" нелинейных эволюционных уравнений определенного типа. Так, если В- непрерывный всюду определенный диссипативный оператор, то задача Коши и=Ви, и(0)=и ₀ однозначно разрешима на полуоси J⁺ при любом 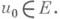Определение диссипатпвного оператора естественно переносится на случай многозначного оператора, и для таких операторов вместо дифференциального уравнения рассматривается дифференциальное включение 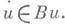Если в рефлексивном пространстве оператор Взамкнут, диссипативен и значения оператора I-Впокрывают все пространство Е, то задача Коши однозначно разрешима на J⁺ при каждом и ₀ из области определения оператора В. Имеется много вариантов последнего утверждения. Решение задается формулой u(t)= S(t)u₀, где S(t)- полугруппа нелинейных операторов S(t+t)x=S(t)(S(t)х), t, Для уравнений с диссипативными операторами имеются также теоремы существования периодич. и почти периодич. решений.

Лит.:[1] Далецкий Ю. Л., Крейн М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970; [2] Массера Х.-Л., Шефер Х.-Х., Линейные дифференциальные уравнения и функциональные пространства, пер. с англ., М., 1970; [3] Иосида К., Функциональный анализ, пер. с англ., М., 1967; [4] Крейн С. Г., Линейные дифференциальные уравнения в банаховых пространствах, М., 1967; [5] Вarbu V., Nonlinear semigroups and differential equations in banach spaces, Netherlands, 1976; [6] Баскаков А. Г., "Тр. матем. ф-та Воронеж, ун-та", 1973, в. 10, с. 96-101; [7] Жиков В. В., "Изв. АН "СССР. Сер. матем.", 1976, т. 40, с. 1380-1408, № 6; [8] Жиков В. В., Левитан Б. М., "Успехи матем. наук", 1977, т. 32, в. 2, с. 123-71; [9] Милославский А. И., "Функц. анализ и его прилож.", 1976,т. 10, № 2, с. 80-81; [10] Тюрин В. М., в кн.: "Функциональный анализ", в. 1, Ульяновск, 1973; [11] Левитан Б. М., Жиков В. В., Почти периодические функции и дифференциальные уравнения, М., 1977.

С. Г. Крейн.