Akademik

однопараметрическое семейство операторов S(t),0t<, определенных и действующих в замкнутом подмножестве Сбанахова пространства X, обладающее свойствами:

1) S(t+t)x= S(t)(S(t)x).при х С, t,t>0;

2) S(Q)x=x для любого х С;

3) при каждом х Сфункция S(t)x(со значениями в X).непрерывна по tна [0, ). Полугруппа S(t).имеет тип w, если

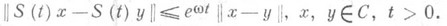
Полугруппа типа 0 наз. сжимающей.

Так же, как и для полугрупп линейных операторов, вводится понятие производящего оператора А ₀ полугруппы S(t).

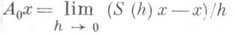
на тех элементах 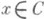, для к-рых этот предел существует. Если полугруппа сжимающая, то А ₀- диссипативный оператор. При этом оператор Ав банаховом пространстве Xдиссипативен, если || х-у-l( Ах-Ау)||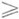||х-у|| при 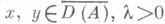. Диссипативный оператор может быть многозначным, тогда в определении под Ах понимается любое его значение на х. Диссипативный оператор наз. m-диссипативным, если lm (I-lА)=Х при l>0. Если S(t) - типа w, то A₀-wI диссипативен.

Основная теорема о порождении полугруппы: если оператор А-wI диссипативен и при достаточно малых l>0 образ Im (I-lA) оператора I-lАсодержит D(А), то существует полугруппа S_A(t) типа со на 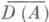такая, что

где 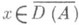, при этом сходимость равномерна на любом конечном промежутке изменения t. (Существование полугруппы S_A(t).можно показать, если заменить условие 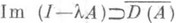более слабым:

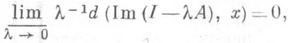
где d - расстояние между множествами.)

С оператором Аможно связать задачу Коши

(*)

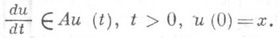Если существует сильное решение задачи (*), т. е. непрерывная на [0, ) функция u(t), абволютно непрерывная на любом компакте из (0, 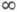), принимающая при почти всех t>0 значения в D(A), имеющая при почти всех t>0 сильную производную, удовлетворяющую включению (*), то u(t)=S_A(t)x. Любая функция S_A(t)хявляется единственным т. н. интегральным решением задачи (*).

Если в условиях основной теоремы пространство Xрефлексивно и Азамкнут, то при х D (А).функция u(t)=S_A(t).дает сильное решение задачи Коши (*), при этом 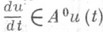почти везде, где A⁰z - множество элементов минимальной нормы из Az. В этом случае производящий оператор А ₀ полугруппы S_A(t).плотно задан: 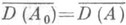. Если, сверх того, Xи X' равномерно выпуклы, то оператор А ⁰ однозначен и при всех существует правая производная 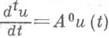; эта функция непрерывна справа на [0, ) и непрерывна во всех точках, кроме, быть может, счетного множества, в этом случае D(A₀) = D(A).и А ₀=А ⁰.

Если Xрефлексивно (соответственно X=Y', где Y - сепарабельно), а оператор Аоднозначен и обладает тем свойством, что из 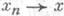в Xи 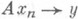в слабой топологииs( Х, X').(соответственно s( Х, Y)) следует у=Ах, то 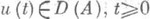и u(t).слабо (соответственно слабо *) непрерывно дифференцируемое решение задачи (*). В нерефлексивном случае известны примеры, когда выполнены условия основной теоремы при 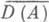==Х и функции u(t) = S_A(t)xне имеют даже слабой производной в Xни при каких .

Пусть А- непрерывный оператор, определенный на всем Xи такой, что А-wI диссипативен. Тогда Im(I-lА)=X при l>0, lw <1 и для любого 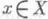задача (*) имеет единственное непрерывно дифференцируемое на [0, ) решение и(t)=S_A(t)x. Если оператор Анепрерывен в замкнутой области определения D(A), то для того, чтобы он был производящим оператором полугруппы типа w на D(А), необходимо и достаточно, чтобы А-wI был диссипативным и 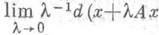,D(A))=0 при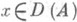

В гильбертовом пространстве Нсжимающая полугруппа на множестве Сможет быть продолжена для сжимающей полугруппы на замкнутом выпуклом множестве из Н. При этом производящий оператор А ₀ расширенной полугруппы будет определен на плотном в 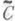множестве. Существует единственный m-диссипативный оператор такой, что 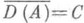и А ₀=А ⁰. Если Аесть m-диссипативнын оператор, то выпукло и существует единственная сжимающая на 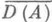полугруппа S(t)=S_A(t), для к-рой A₀=A⁰.

Если на действительном гильбертовом пространстве Нзадан выпуклый полунепрерывный функционал j и дj - его субдифференциал, то оператор Ax=-дj(x) (для тех x, при к-рых дj(х).непусто) является диссипативным. Полугруппа S_A(t).обладает свойствами, сходными со свойствами линейных аналитич. олугрупп. В частности, 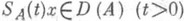при любом 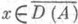и u(t)=S_A(t)xявляется сильным решением задачи Коши (*), причем

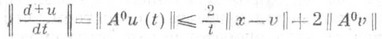
для всех . Если j достигает минимума, то и(t).слабо сходится при 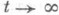к нек-рой точке минимума .

Для приближенного решения задачи Коши существенную роль играют теоремы об аппроксимации полугрупп. Пусть X, Х _n, n=1, 2, ...,- банаховы пространства, операторы Ав Х и А _n в Х _п однозначны и удовлетворяют условиям основной теоремы с общим типом ш, операторы 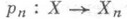- линейны и 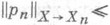const. Тогда из сходимости резольвент (l>0, lw<1)

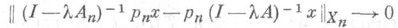
при 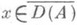следует сходимость полугрупп

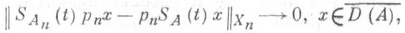
равномерная на каждом конечном промежутке. Мультипликативные формулы Ли, полученные им в конечномерном линейном случае, обобщены на нелинейный случай. Если А, В и А +В суть m-диссипативные однозначные операторы в гильбертовом пространстве и замкнутое выпуклое множество 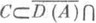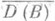инвариантно относительно (I-lА)^-1 и (I-lВ)^-1, то при любом

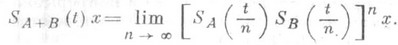
Эта формула справедлива также в произвольном банаховом пространстве Xдля любого 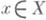, если А - плотно заданный линейный m-диссипативный оператор, а В - заданный на всем Xнепрерывный диссипативный оператор. В обоих случаях

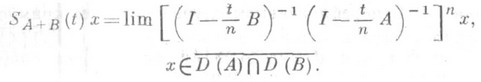
В приводимых ниже примерах нелинейных дифференциальных операторов, удовлетворяющих условиям основной теоремы о порождении полугрупп, указывается лишь пространство Xи краевые условия, а точное описание D(А).опускается. Во всех примерах W - ограниченная область в с гладкой границей; b, g - многозначные максимальные монотонные отображения 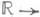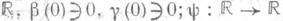- непрерывная строго возрастающая функция, y(0)=0. Пример 1.

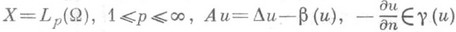на Г.

Пример 2. 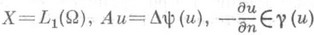на Г.

Пример 3. 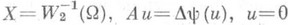на Г. Пример4. 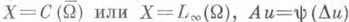, u=0 на Г.

Пример 5. 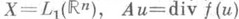, где со значениями в .

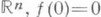Пример 6. , где 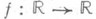непрерывна. Лит.:[1] Вarbu V., Nonlinear semigroups and differential equations_ in Banach spaces, Bucurejti, 1976; [2] Вrezis H., Operateurs maximaux monotones et semi-groupes de contractions dans les espaces de Hilbert, Amst.-L.-N.Y., 1973; [3] Brezis H., Pazу A., "J. Funct. Anal.", 1972, v. 9, № 1, p. 63-74; [4] Сrandall M. G., Liggett Т. М., "Amer. J. Math.", 1971, v. 93, № 2, p. 265-98; [5] Коbayashi Y., "J. Math. Soc. Japan", 1975, v. 27, № 4, p. 640-65; [6] Konishi Y., "Proc. Japan. Acad.", 1972, v. 48, №2, p. 62-66; [7] Martin R. H., "Trans. Amer. Math. Soc.", 1973, v. 179, p. 399-414; [8] Webb G. F., "J. Funct. Anal", 1972, v. 10, №2, p. 191-203; [9] Хазан М. И., "Докл. АН СССР", 1973, т. 212, №6, с. 1309-12; [10] его ж е, там же, 1976, т. 228, М 4, с. 805-808.

С. Г. Крейн, М. И. Хазан.