Akademik

PERCOLATION

La percolation est un problème de communication qui se pose dans un milieu étendu dans lequel sont distribués régulièrement un grand nombre de «sites» susceptibles de relayer localement une information. Ceux-ci communiquent entre eux par des liens dont l’efficacité est aléatoire. Suivant que la proportion de liaisons actives est ou non supérieure à une valeur seuil, il existe ou non une possibilité de transmettre l’information à grande distance.

La caractéristique de la percolation réside dans le fait qu’il s’agit d’un phénomène critique: au-dessous du seuil, une information reste confinée dans le petit îlot où elle est née; sitôt dépassé le seuil, l’information «percole» et se retrouve aussi loin de son point de départ qu’on aille la chercher. Le terme information est pris ici dans son sens le plus large; il peut s’agir d’une propriété physique ou biologique aussi bien que d’un fluide. Le mot percolation a été introduit par le mathématicien anglais J. M. Hammersley en 1957 pour décrire le passage d’un fluide à travers un milieu poreux. Il est également employé, dans un sens très différent de celui que nous lui donnons ici, en géochimie et en génie chimique pour définir des processus comportant des échanges entre un fluide et le milieu traversé.

L’établissement, en 1969, par P. W. Kasteleyn et C. M. Fortuin d’un théorème permettant une correspondance rigoureuse entre les grandeurs de la percolation et celles des transitions de phase la fait entrer dans le cadre de ces dernières et lui offre le bénéfice des nombreux résultats obtenus dans ce domaine.

La percolation permet de décrire un grand nombre de phénomènes physiques, biologiques ou sociologiques au moyen des mêmes concepts géométriques et statistiques.

Modèles

Un système de communication rapide à grande distance peut être constitué par un réseau de stations, placées sur des hauteurs, à partir desquelles des opérateurs relaient des signaux optiques. Chaque station est en vue de plusieurs autres. L’ennemi fondamental du système est le manque de visibilité pour cause météorologique, coupant le lien entre deux stations. Dans ce cas, il est encore possible de faire passer le signal entre des points très éloignés en utilisant des chemins détournés, mais il est nécessaire, pour cela, que le pourcentage de liens actifs soit supérieur au seuil de percolation. Le problème ainsi décrit ne concerne que les liens entre stations, c’est le problème de la percolation de lien. Mais il est également possible d’envisager une situation de temps clair généralisé dans laquelle certains observateurs seraient distraits ou... endormis. Le problème ainsi posé est celui de la percolation de site. Il présente aussi un seuil, qui est dans ce cas le pourcentage de sites actifs en dessous duquel l’information ne percole pas d’un bout à l’autre du réseau. La réalité tient à la fois de l’un et de l’autre problème; sa représentation est un graphe à deux dimensions (fig. 1). Il existe des cas particuliers simples où ce graphe est un réseau régulier (fig. 2). Celui-ci permet une simulation numérique de type Monte-Carlo du problème: il suffit de créer les liens (ou les sites) avec une probabilité p et d’examiner la situation obtenue lorsque p varie de 0 à 1. On observe que les sites, d’abord isolés, se groupent ensuite en doublets, triplets... puis forment des «amas» plus gros, ramifiés, lacunaires. Au seuil, quelques liens supplémentaires suffisent pour associer brusquement plusieurs de ces amas en un seul: l’amas infini, qui atteint les frontières de l’échantillon, si grand soit-il (fig. 3).

La percolation transition de phase

Le modèle sur réseau à deux dimensions (d = 2) est schématique. Un problème de percolation se définit plus généralement dans un espace à d dimensions pour un milieu hétérogène composé d’éléments de propriétés très différentes et montrant, à grande échelle, un comportement homogène original caractérisé par:

– L’existence d’un seuil, qui dépend du problème et du réseau.

– L’existence d’une échelle de longueur caractéristique grande devant le pas du réseau. Au-dessous du seuil, un parachutiste largué sur un site actif et passant de site actif en site actif restera toujours à une distance finie de son point de départ. Au contraire, au seuil, il pourra s’éloigner infiniment. Son rayon d’action est caractérisé par la longueur de corrélation 﨡; celle-ci devient infinie au seuil, dans le voisinage duquel elle suit une loi de variation critique: 﨡 力 﨡⁰|p 漣 p ^c |^- size=1^益.

À cette connexion entre sites très éloignés, il est possible d’associer, dans un aimant, l’ordre à grande distance de l’orientation des moments magnétiques en dessous de la température de Curie ^C. Dans ce cas, le paramètre d’ordre est l’aimantation M qui, au voisinage de ^C, a une variation critique M = M⁰(T^C 漣 T) size=1^廓. On lui fait correspondre, en percolation, la proportion de sites actifs contenus dans l’amas infini: P = B(p 漣 p ^C) size=1^廓. Elle s’exprime au moyen du premier moment de la distribution statistique des amas. Il existe des analogies équivalentes pour les autres moments.

Les exposants critiques, 益, 廓, ..., qui décrivent les comportements singuliers dans la transition de percolation, sont universels. Ils ne dépendent pas des caractères locaux du problème (réseau, désordre...), puisqu’on doit effectuer la moyenne sur la taille caractéristique 﨡, mais seulement de la dimension de l’espace où on le définit (en percolation à d = 2, 廓 = 0,14, 益 = 4/3, et à d = 3, 廓 = 0,4, 益 = 0,8).

Les modèles se sont affinés et multipliés au cours du temps. En percolation corrélée, l’activité d’un site ou d’un lien n’est plus indépendante de celle de ses voisins: un arbre dans une forêt en feu ne brûle que si plus d’un de ses voisins est en flammes. En percolation anisotrope, la probabilité d’existence des liens est plus grande dans un sens, par exemple celui du champ électrique dans certaines céramiques dont la résistance s’annule pour de fortes différences de potentiel. La percolation brassée tient compte du fait que les amas sont dynamiques: dans une suspension sous cisaillement, les amas se forment et se désagrègent continuellement.

Méthodes

L’intérêt, d’abord porté à la détermination des seuils, s’est ensuite déplacé sur les exposants critiques. Actuellement, l’approche de percolation se généralise dans l’étude des propriétés de transport (passage du courant électrique, conduction de la chaleur...). L’amas infini et sa structure font l’objet du plus grand nombre de travaux. En effet, l’amas infini possède la particularité d’être «self-similaire»: un détail vu de près a le même aspect que l’ensemble vu de loin (photos a et b), il a une dimension fractale qui caractérise son comportement vis-à-vis de ces phénomènes.

Les résultats théoriques proviennent de trois sources: d’abord celle des développements en série, qui consiste à déterminer par comptage direct la statistique d’amas sur réseau pour de petits échantillons et à l’extrapoler au moyen de développements mathématiques; ensuite, la méthode de renormalisation; enfin, et surtout, les simulations numériques par méthodes de Monte-Carlo. Ces dernières se sont diversifiées et ne se limitent plus à la détermination des statistiques d’amas. Une d’elles (la fourmi dans un labyrinthe), simulant une marche aléatoire sur un réseau de liens, permet d’étudier la diffusion à deux et trois dimensions dans un milieu poreux ou de déterminer l’exposant de la conductivité.

Certains résultats obtenus par des expériences réelles sont à l’origine d’extensions déterminantes de la théorie. C’est le cas pour la conduction électrique.

Les milieux poreux offrent un exemple de la façon dont la percolation prend le relais des méthodes classiques. Un poreux peut se boucher de deux façons: ou bien il s’entartre, tous les pores se rétrécissent à la fois, et la perméabilité décroît régulièrement; ou bien des impuretés contenues dans le fluide bloquent complètement les pores dont le diamètre est plus petit que le leur, et il y a alors un blocage pour une valeur non nulle de la porosité. Les lois classiques rendent compte du premier processus, la percolation du second.

Quelques applications

L’utilisation de la théorie de la percolation pour résoudre un problème physique comporte deux étapes: tout d’abord le choix d’un modèle de percolation qui simule convenablement le phénomène; ensuite, la détermination des propriétés de ce modèle par l’une des méthodes que nous venons d’évoquer.

Les matériaux hétérogènes, qui présentent un désordre de position et de composition, correspondent bien à la description d’un milieu dans lequel il est possible de définir un modèle de percolation. Ce sont les alliages, les gels, les composites, les milieux poreux...

Citons quelques applications dans ce domaine:

– Certaines céramiques ou les caoutchoucs chargés sont formés d’éléments conducteurs et isolants disposés aléatoirement. Ils sont isolants tant que la proportion de conducteurs est inférieure au seuil, où ils deviennent brusquement conducteurs. Leur conductivité 靖 varie ensuite comme (p 漣 p ^C)^t , t étant un exposant critique de transport (à d = 2, t = 1,3). L’étude de la réponse en fréquence de ces milieux est fondée sur le caractère fractal de l’amas infini conducteur. Le comportement des céramiques parafoudre relève de la percolation dirigée.

– Dans la transition de gélification (la prise d’une gélatine par exemple), des éléments polymériques s’associent pour former un réseau tridimensionnel. Au seuil de gélification (correspondant au seuil de percolation) apparaît un amas infini (le gel). On associe à la masse du gel la notion de paramètre d’ordre (exposant 廓), l’élasticité du gel pouvant être reliée à l’exposant t de la conductivité.

On utilise la percolation dans l’étude des milieux poreux dans plusieurs cas, citons-en deux:

– celui des milieux mal connectés au voisinage d’un seuil de perméabilité (roches faiblement fissurées);

– celui dans lequel deux phases non miscibles sont en présence dans le milieu poreux (eau et air en hydrogéologie) et où il existe des seuils de continuité pour l’une et l’autre phase.

Ouvertures

La fragilité des matériaux ou leur fatigue, la propagation des fissures et des fractures peuvent être interprétées en termes de percolation. Un désordre local peut en effet induire un désordre général et entraîner la rupture du matériau. Un modèle de percolation non linéaire est alors appliqué, la connaissance des propriétés locales ne suffisant plus pour décrire le comportement global.

Mise au point par les physiciens, la percolation a cependant un champ d’applications qui déborde largement la physique; par exemple, on conçoit sans peine que la propagation des épidémies ou la prolifération des tumeurs puisse se formuler en termes de percolation.

• 1903; de percolateur

♢ Phys. Transition de percolation ou percolation : transformation structurelle d'un mélange lorsque la proportion de l'un des constituants atteint un seuil critique. Transition de percolation d'un sol en gel.

n. f. PHYS Circulation de l'eau à travers un milieu poreux.

⇒PERCOLATION, subst. fém.

1.— Technique de raffinage des huiles de pétrole par passage sur une matière absorbante. (Dict. XX^e s.).

2. Traitement d'une substance par des solvants et des passages dans des filtres pour la purifier ou en extraire certains produits. Synon. lixiviation. Des cuves, parfois extrêmement vastes comme dans la cyanuration des minerais d'or, laisseront les liqueurs d'attaque traverser les grains maintenus à une certaine distance du fond par une toile filtrante qui laisse passer le liquide; il y a alors percolation (GUILLET, Techn. métall., 1944, p. 97).

3. Circulation d'un fluide sous pression à travers une substance pour extraire de celle-ci un arôme ou une essence (d'apr. SALLÉ 1982).

1. Mouvement de l'eau traversant lentement un terrain perméable (d'apr. COLAS-CAB. 1968).

2. Procédé de culture artificielle sans sol, où les substances nutritives sont apportées par des solutions traversant le support de haut en bas (d'apr. LEMAIRE Envir. 1975).

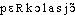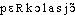Prononc. :[]. Étymol. et Hist. 1923 (GUILLET, Métall. gén., p. 402). Empr. au lat. percolatio « filtration ».

percolation [pɛʀkɔlɑsjɔ̃] n. f.

ÉTYM. 1903, Rev. gén. des sc., n^o 10, p. 548; du rad. de percol(ateur).

❖

1 Techn. Procédé de raffinage (huiles de pétrole, de lin) par circulation dans une matière adsorbante.

➪ tableau Vocabulaire de la chimie.