Akademik

ЛАГРАНЖА ФУНКЦИЯ

ЛАГРАНЖА ФУНКЦИЯ: (кинетический потенциал), характеристич. функция L(qi, q'i, t) механич. системы, выраженная через обобщённые координаты qi, обобщённые скорости q'i и время t. В простейшем случае консервативной системы Л. ф. равна разности между кинетич. Т и потенциальной П энергиями системы, выраженными через qi и q'i, т. е. L=T(qi, q'i,t) -Пqi;. Зная Л. ф., можно с помощью наименьшего действия принципа составить дифф. ур-ния движения механич. системы.

Понятие «Л. ф.» распространяется также на системы с бесконечным числом степеней свободы — классические поля физические; при этом обобщёнными координатами и импульсами явл. значения ф-ции поля и их производные по времени в каждой точке пространства-времени. Как и в классич. механике, посредством принципа наименьшего действия Л. ф. определяет для поля ур-ния движения. Важным св-вом Л. ф. явл. релятивистская инвариантность её плотности (величины Л. ф. в ед. объёма поля) и др. св-ва её симметрии. Каждой из симметрии соответствует закон сохранения нек-рой физ. хар-ки. Так, неизменности относительно калибровочной симметрии соответствует сохранение заряда и т. д. (см. СОХРАНЕНИЯ ЗАКОНЫ).

ЛАГРАНЖА ФУНКЦИЯ: (кинетический потенциал) - характеристич. функция L(q_i, 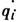, t )механич. системы, выраженная через обобщённые координаты q_i, обобщённые скорости q_i и время t. В простейшем случае консервативной системы Л. ф. равна разности между кинетической Т и потенциальной П энергиями системы, выраженными через q_i и q_i, т. е. L=T(q_i,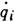, t) - П (q_i). Зная Л. ф., можно с помощью наименьшего действия принципа составить дифференциальные ур-ния движения механич. системы. Понятие о Л. ф. распространяется и на др. физ. системы (см. Лагранжиан, Лагранжа уравнения механики 2-го рода, Лагранжев формализм).