Akademik

ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ

ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ: Принципами механики наз. исходные положения, отражающие столь общие закономерности механич. явлений, что из этих положений как следствия можно получить ур-ния, определяющие движения механич. системы (или условия её равновесия). В механике установлен ряд таких принципов, каждый из к-рых может быть положен в её основу и к-рые подразделяют на невариационные и вариационные.

Невариац. принципы механики непосредственно устанавливают закономерности движения, совершаемого системой под действием приложенных к ней сил. К ним относится, напр., 2-й закон Ньютона, Д'Аламбера принцип. Невариац. принципы справедливы для любой механич. системы и имеют сравнительно простое матем. выражение. Однако их применение ограничено только рамками механики, поскольку в выражения принципов непосредственно входит такое чисто механич. понятие, как сила. Существенно также, что в большинстве задач механики рассматривается движение несвободных систем, т. е. систем, перемещения к-рых ограничены связями (см. СВЯЗИ МЕХАНИЧЕСКИЕ), напр. всевозможные машины, механизмы, наземный транспорт, где связями явл. подшипники, шарниры, тросы, полотно дороги или рельсы и т. п. Исходя из невариац. принципов при изучении движения несвободной системы эффект действия связей учитывают введением нек-рых сил, наз. реакциями связей, величины к-рых заранее неизвестны, поскольку они зависят от того, чему равны и где приложены действующие на систему заданные (активные) силы, такие, напр., как сила тяжести, упругости пружин, тяги, а также от того, как при этом движется сама система. Поэтому в составленные ур-ния движения войдут дополнит. неизвестные величины — реакции связей, что обычно существенно усложняет решение этих ур-ний.

Преимущество В. п. м. состоит в том, что из них сразу получаются ур-ния движения соответствующей механич. системы, не содержащие неизвестных реакций связей. Достигается это тем, что эффект действия связей учитывается не заменой их неизвестными силами (реакциями), а рассмотрением тех перемещений и движений (или приращений скоростей и ускорений), к-рые точки этой системы могут иметь при наличии данных связей. Напр., если точка М движется по гладкой (идеальной) поверхности, являющейся для неё связью (рис. 1), то действие этой связи можно учесть, заменив связь заранее неизвестной по величине реакцией N, направленной в любой момент времени по нормали Mn к поверхности (поскольку по этому направлению связь не даёт перемещаться точке). Но эффект этой же связи можно учесть, установив,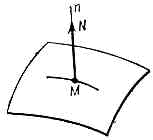

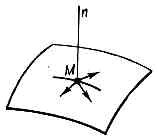
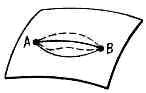Рис. 1. Рис. 2. Рис. 3.

что для точки М в данном случае при любом её положении возможны лишь элементы перемещения, перпендикулярные к нормали Mn (рис. 2); такие перемещения наз. возможными перемещениями. Наконец, эффект той же связи может быть охарактеризован и тем, что при этом движение точки из нек-рого положения А в положение В возможно только по любой кривой АВ, лежащей на поверхности, к-рая явл. связью (рис. 3); такие движения наз. кинематически возможными.

Содержание В. п. м. состоит в том, что они устанавливают св-ва (признаки), позволяющие отличить истинное, т. е. фактически происходящее под действием заданных сил, движение механич. системы от тех или иных кинематически возможных её движений (или же состояние равновесия системы от др. возможных её состояний). Обычно эти св-ва (признаки) состоят в том, что для истинного движения нек-рая физ. величина, зависящая от хар-к системы, имеет наименьшее значение по сравнению с её значениями во всех рассматриваемых кинематически возможных движениях. При этом В. п. м. могут отличаться друг от друга видом указанной физ. величины и особенностями рассматриваемых кинематически возможных движений, а также особенностями самих механич. систем, для к-рых эти В. п. м. справедливы. Использование В. п. м. требует применения методов вариац. исчисления.

По форме В. п. м. разделяют на т. н. дифференциальные, в к-рых устанавливается, чем истинное движение системы отличается от кинематически возможных движений в каждый данный момент времени, и интегральные, в к-рых это различие устанавливается для перемещений, совершаемых системой за к.-н. конечный промежуток времени. Дифференциальные В. п. м. в рамках механики явл. более общими и справедливы для любых механич. систем. Интегральные В. п. м. в их наиболее употребит. виде справедливы только для консервативных систем. Однако в них, в отличие от дифференциальных В. п. м. и невариац. принципов, вместо сил входит такая физ. величина, как энергия, что позволяет распространить эти В. п. м. и на немеханич. явления. К осн. дифференциальным В. п. м. относятся: возможных перемещений принцип, Д'Аламбера — Лагранжа принцип, Гаусса принцип (принцип наименьшего принуждения), а также тесно примыкающий к нему Герца принцип (принцип наименьшей кривизны). К интегральным В. п. м. относятся т. н. принципы наименьшего (стационарного) действия, разные формы к-рых отличаются друг от друга выбором величины действия и особенностями сравниваемых между собой кинематически возможных движений системы (см. НАИМЕНЬШЕГО ДЕЙСТВИЯ ПРИНЦИП). Применяются В. п. м. как для составления в наиболее простой форме ур-ний движения механич. систем, так и для изучения общих св-в этих движений. При соответствующем обобщении понятий они используются также в механике сплошных сред, термодинамике, электродинамике, квант. механике, теории относительности и др.