Akademik

ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ

ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ: (Черенкова -- Вавилова эффект), излучение света электрически заряженной ч-цей, возникающее при её движении в среде с пост. скоростью v, превышающей фазовую скорость света в этой среде (скорость распространения световых волн). Обнаружено в 1934 при исследовании П. А. Черенковым g-люминесценции р-ров как слабое голубое свечение жидкостей под действием g-лучей. Эксперименты Черенкова, предпринятые по инициативе С. И. Вавилова, выявили характерные особенности излучения: 1) свечение наблюдается у всех чистых прозрачных жидкостей, причём его яркость мало зависит от их хим. состава; 2) излучение имеет поляризацию с преим. ориентацией вектора напряжённости электрич. поля вдоль направления первичного пучка; 3) в отличие от люминесценции, не наблюдается ни температурного, ни примесного тушения. На основании этих данных Вавилов сделал основополагающее утверждение, что обнаруженное явление — не люминесценция, свет же излучают движущиеся в жидкости быстрые эл-ны, образующиеся при облучении в-ва. Ч.— В. и характерно не только для жидкостей, но и для тв. тел и газов. Свечение, вызываемое g-излучением, нек-рые учёные наблюдали и раньше (напр., франц. учёный М. Л. Малле, в 1926 — 1929 получивший фотографии его спектра). Однако оставалось непонятным то, что наблюдаемое излучение — новое, ещё не изучавшееся явление; не было установлено и наиб. характерное его св-во, обнаруженное Черенковым в 1936,— направленность под острым углом к скорости ч-цы.

Механизм Ч.— В. и. был выяснен в работе И. Е. Тамма и И. М. Франка (1937), содержавшей и количеств. теорию, основанную на ур-ниях классич. электродинамики. К тем же результатам привело и квант. рассмотрение (В. Л. Гинзбург, 1940).

Условие возникновения Ч.— В. и. и его направленность могут быть пояснены с помощью Гюйгенса принципа.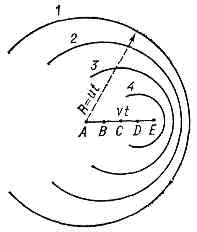

Рис. 1. Движение заряж. ч-цы в среде со скоростью v

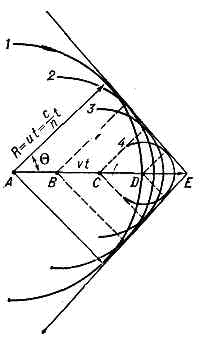Рис. 2. Движение заряж. ч-цы в среде со скоростью v>u. Угол между направлениями волнового вектора возникающего излучения и скоростью ч-цы равен q.

Каждую точку (А, В, С, D на рис. 1 и 2) траектории заряж. ч-цы следует считать источником волны, возникающей в момент прохождения через неё ч-цы. В оптически изотропной среде такие парциальные волны будут сферическими, распространяющимися со скоростью u=c/n, где n — показатель преломления среды. Допустим, что ч-ца, двигаясь равномерно и прямолинейно со скоростью v, в момент наблюдения находилась в точке Е. За время t до этого она проходила через точку A (AE=vt). Волна, испущенная из А, к моменту наблюдения представится сферой радиуса R=ut; на рис. 1 и 2 ей соответствует окружность 1, а волнам, испущенным из В, С, D,— окружности 2, 3, 4. По принципу Гюйгенса в результате интерференции парциальные волны гасят друг друга всюду за исключением их общей огибающей, к-рой соответствует волн. поверхность света, распространяющегося в среде.

Пусть v и (рис. 1), тогда световые волны будут обгонять ч-цу на тем большее расстояние, чем раньше они испущены. Общей огибающей парциальные волны при этом не имеют — все окружности 1, 2, 3, 4 лежат одна внутри другой; следовательно, электрич. заряд при равномерном и прямолинейном движении со скоростью v

Если же ч-ца движется быстрее, чем распространяются световые волны, т. е. при

v>u = c/n, или bn>1 (1)

(где b=v/c), то соответствующие волнам сферы пересекаются (рис. 2), их общая огибающая (волновая поверхность) представляет собой конус с вершиной в точке Е, совпадающей с мгновенным положением ч-цы, а нормали к образующим конуса определяют волн. векторы, т. е. направления распространения света. Угол 6, к-рый составляет волн. вектор с направлением движения ч-цы (см. рис. 2), удовлетворяет отношению:

cosq=u/v=c/nv=l/bn. (2)

Такой же метод рассмотрения можно провести и для оптически анизотропной среды (в частности, для прозрачных кристаллов), в к-рой парциальные волны не явл. сферами. В этом случае обыкновенному и необыкновенному лучам будут соответствовать разные конусы и излучение будет возникать под разными углами 6 к направлению распространения ч-цы, согласно соотношению (2). Условие (1) для оптически анизотропных сред формулируется неск, иначе. Во всех случаях осн. ф-лы теории хорошо согласуются с опытом.

Расчёт показывает, что в оптически изотропной среде ч-ца с зарядом е, прошедшая расстояние в 1 см со скоростью v > и, излучает энергию:

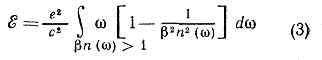(w=2pc/l — круговая частота света, l — дл. волны излучаемого света в вакууме). Подынтегральное выражение отражает распределение энергии в спектре Ч.— В. и.

В жидкостях и тв. в-вах условие (1) начинает выполняться для эл-нов уже при энергиях =105 эВ, для протонов, масса к-рых в =2000 раз больше электронной,— при энергиях =108 эВ. На основе Ч.— В. и. разработаны широко применяемые эксперим. методы для регистрации ч-ц высоких энергий, измерения их скорости. Приборы, применяемые для этой цели, наз. черенковскими счётчиками. Эти методы позволяют также рассчитывать массу ч-ц (это, напр., было использовано при открытии антипротона).

Ч.— В. и. может наблюдаться в чистом виде только в идеальных случаях, когда заряж. ч-ца движется с пост. скоростью в радиаторе неогранич. длины. В тонком радиаторе, удовлетворяющем условию (1), Ч.— В. и. неотделимо от переходного излучения, возникающего при пересечении ч-цей границы раздела 2 сред с разными коэфф. преломления.

В 1940 Э. Ферми обобщил теорию Ч.— В. и., приняв во внимание, что реальная среда обладает способностью поглощать свет по крайней мере в нек-рых областях спектра. Полученные им результаты внесли существ. уточнения в теорию ионизац. потерь заряж. ч-цами (эффект поляризации среды).

Ч.— В. и. явл. примером оптики «сверхсветовых» скоростей и имеет принципиальное значение. Ч.— В. и. экспериментально и теоретически изучено не только в оптически изотропных средах, но и в кристаллах, теоретически рассмотрено излучение электрич. и магн. диполей и мультиполей. Ожидаемые св-ва излучения движущегося магн. заряда были использованы для поисков магнитного монополя. Рассмотрено излучение ч-цы в канале внутри среды (напр., излучение пучка ч-ц внутри волновода) и др. Новые особенности приобретает Доплера эффект в среде: появляются т. н. аномальный и сложный Доплера эффекты. Можно полагать, что всякая система ч-ц, способная взаимодействовать с эл.-магн. полем, будет излучать свет за счёт своей кинетич. энергии, если её скорость превышает фазовую скорость света.

Теор. представления, лежащие в основе Ч.— В. и., тесно связаны с др. явлениями, имеющими важное значение в совр. физике (волны Маха в акустике, вопросы устойчивости движения ч-ц в плазме и генерации в ней волн, нек-рые проблемы теории ускорителей, а также генерация и усиление эл.-магн. волн).