- ТЕПЛОПРОВОДНОСТЬ
-
один из видов переноса теплоты от более нагретых частей тела к менее нагретым, приводящий к выравниванию темп-ры. При Т. перенос энергии осуществляется в результате непосредств. передачи энергии от ч-ц (молекул, атомов, эл-нов), обладающих большей энергией, ч-цам с меньшей энергией. Если относит. изменение темп-ры Т на расстоянии ср. длины свободного пробега ч-ц l мало, то выполняется осн. закон Т. (закон Фурье): плотность теплового потока q пропорциональна градиенту темп-ры grad Т: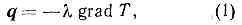 где l — коэфф. Т., или просто Т., не зависит от grad Т (l зависит от агрегатного состояния в-ва, его атомно-молекулярного строения, темп-ры, давления, состава и т. д.).Отклонения от закона Фурье могут появиться при очень больших значениях grad Т (напр., в сильных ударных волнах), при низких температурах (для жидкого Не II) и при темп-рах =104—105 К, когда в газах перенос энергии осуществляется не только в результате межатомных столкновений, но в основном за счёт излучения (лучистая Т.). В разреженных газах, когда l сравнимо с расстоянием L между стенками, ограничивающими объём газа, молекулы чаще сталкиваются со стенками, чем между собой. При этом нарушается условие применимости закона Фурье и само понятие локальной темп-ры газа теряет смысл. В этом случае рассматривают не процесс Т. в газе, а теплообмен между телами, находящимися в газовой среде. Процесс Т. в сплошной среде описывается теплопроводности уравнением. Для идеального газа, состоящего из тв. сферич. молекул диаметром d, согласно кинетической теории газов, справедливо следующее выражение для l
где l — коэфф. Т., или просто Т., не зависит от grad Т (l зависит от агрегатного состояния в-ва, его атомно-молекулярного строения, темп-ры, давления, состава и т. д.).Отклонения от закона Фурье могут появиться при очень больших значениях grad Т (напр., в сильных ударных волнах), при низких температурах (для жидкого Не II) и при темп-рах =104—105 К, когда в газах перенос энергии осуществляется не только в результате межатомных столкновений, но в основном за счёт излучения (лучистая Т.). В разреженных газах, когда l сравнимо с расстоянием L между стенками, ограничивающими объём газа, молекулы чаще сталкиваются со стенками, чем между собой. При этом нарушается условие применимости закона Фурье и само понятие локальной темп-ры газа теряет смысл. В этом случае рассматривают не процесс Т. в газе, а теплообмен между телами, находящимися в газовой среде. Процесс Т. в сплошной среде описывается теплопроводности уравнением. Для идеального газа, состоящего из тв. сферич. молекул диаметром d, согласно кинетической теории газов, справедливо следующее выражение для l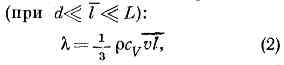 где r — плотность газа, cV — теплоёмкость единицы массы газа при пост. объёме V, v — ср. скорость движения молекул. Поскольку l пропорциональна 1/р, а r= р (р — давление газа), то Т. такого газа не зависит от р. Кроме того, коэффициенты Т. l и вязкости h связаны соотношением: l=5/2hcV. В случае газа, состоящего из многоатомных молекул, существенный вклад в К вносят внутр. степени свободы молекул, что учитывает соотношение:l=hcV((9g-5)/4),где g=cp/cV, cp — теплоёмкость при постоянном р. В реальных газах Т.— довольно сложная ф-ция Т и р, причём с ростом Т и р значение l возрастает. Для газовых смесей l может быть как больше, так и меньше Я компонентов смеси, т. е. Т.— нелинейная ф-ция состава.В плотных газах и жидкостях ср. расстояние между молекулами сравнимо с размерами самих молекул, а кинетич. энергия движения молекул того же порядка, что и потенц. энергия межмолекулярного взаимодействия. В связи с этим перенос энергии столкновениями происходит значительно интенсивнее, чем в разреженных газах, и скорость передачи энергии молекул от горячих изотермич. слоев жидкости к более холодным близка к скорости распространения малых возмущений р, равной скорости звука, т. е. l=rcVusL, где us — скорость звука в жидкости, L — ср. расстояние между молекулами. Эта ф-ла лучше всего выполняется для одноатомных жидкостей. Как правило, Я жидкостей убывает с ростом Т и слабо возрастает с ростом р.Т. тв. тел имеет разл. природу в зависимости от типа тв. тела. В диэлектриках, не имеющих свободных электрич. зарядов, перенос энергии теплового движения осуществляется фононами. У тв. диэлектриков l»cvl, где с — теплоёмкость диэлектрика, совпадающая с теплоёмкостью газа фононов, v= — ср. скорость фононов, приблизительно равная скорости звука, l= — ср. длина свободного пробега фононов. Существование определённого конечного значения l=— следствие рассеяния фононов на фононах, на дефектах крист. решётки (в частности, на границах кристаллитов и на границе образца). Температурная зависимость К определяется зависимостью от темп-ры с и l=.Т. металлов определяется движением и вз-ствием носителей тока -эл-нов проводимости. В общем случае для металла l=lэ+lреш, где lреш и lэ — решёточная фононная и электронная составляющие, причём при обычных темп-рах, как правило, lэ->lреш. В процессе Т. каждый эл-н переносит при наличии grad Г энергию kТ, благодаря чему отношение lэ к электрич. проводимости s в широком интервале темп-р пропорционально Т (Видемана — Франца закон):
где r — плотность газа, cV — теплоёмкость единицы массы газа при пост. объёме V, v — ср. скорость движения молекул. Поскольку l пропорциональна 1/р, а r= р (р — давление газа), то Т. такого газа не зависит от р. Кроме того, коэффициенты Т. l и вязкости h связаны соотношением: l=5/2hcV. В случае газа, состоящего из многоатомных молекул, существенный вклад в К вносят внутр. степени свободы молекул, что учитывает соотношение:l=hcV((9g-5)/4),где g=cp/cV, cp — теплоёмкость при постоянном р. В реальных газах Т.— довольно сложная ф-ция Т и р, причём с ростом Т и р значение l возрастает. Для газовых смесей l может быть как больше, так и меньше Я компонентов смеси, т. е. Т.— нелинейная ф-ция состава.В плотных газах и жидкостях ср. расстояние между молекулами сравнимо с размерами самих молекул, а кинетич. энергия движения молекул того же порядка, что и потенц. энергия межмолекулярного взаимодействия. В связи с этим перенос энергии столкновениями происходит значительно интенсивнее, чем в разреженных газах, и скорость передачи энергии молекул от горячих изотермич. слоев жидкости к более холодным близка к скорости распространения малых возмущений р, равной скорости звука, т. е. l=rcVusL, где us — скорость звука в жидкости, L — ср. расстояние между молекулами. Эта ф-ла лучше всего выполняется для одноатомных жидкостей. Как правило, Я жидкостей убывает с ростом Т и слабо возрастает с ростом р.Т. тв. тел имеет разл. природу в зависимости от типа тв. тела. В диэлектриках, не имеющих свободных электрич. зарядов, перенос энергии теплового движения осуществляется фононами. У тв. диэлектриков l»cvl, где с — теплоёмкость диэлектрика, совпадающая с теплоёмкостью газа фононов, v= — ср. скорость фононов, приблизительно равная скорости звука, l= — ср. длина свободного пробега фононов. Существование определённого конечного значения l=— следствие рассеяния фононов на фононах, на дефектах крист. решётки (в частности, на границах кристаллитов и на границе образца). Температурная зависимость К определяется зависимостью от темп-ры с и l=.Т. металлов определяется движением и вз-ствием носителей тока -эл-нов проводимости. В общем случае для металла l=lэ+lреш, где lреш и lэ — решёточная фононная и электронная составляющие, причём при обычных темп-рах, как правило, lэ->lреш. В процессе Т. каждый эл-н переносит при наличии grad Г энергию kТ, благодаря чему отношение lэ к электрич. проводимости s в широком интервале темп-р пропорционально Т (Видемана — Франца закон):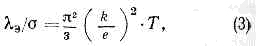 где е — заряд эл-на. В связи с тем, что у большинства металлов lреш-lэ, в (3) можно с хорошей точностью заменить lэ на l. Обнаруженные отклонения от равенства (3) нашли свое' объяснение в неупругости столкновений эл-нов. У полуметаллов Bi и Sb lреш сравнима с lэ, что связано с малостью числа свободных эл-нов в них. Явление переноса теплоты в полупроводниках сложнее, чем в диэлектриках и металлах, т. к. для них существенны и lэ, и lреш, а также в связи со значит. влиянием на l примесей, процессов биполярной диффузии, переноса экситонов и др. факторов. Влияние р на l тв. тел с хорошей точностью выражается линейной зависимостью l от р, причём у мн. металлов и минералов Я растёт с ростом р.
где е — заряд эл-на. В связи с тем, что у большинства металлов lреш-lэ, в (3) можно с хорошей точностью заменить lэ на l. Обнаруженные отклонения от равенства (3) нашли свое' объяснение в неупругости столкновений эл-нов. У полуметаллов Bi и Sb lреш сравнима с lэ, что связано с малостью числа свободных эл-нов в них. Явление переноса теплоты в полупроводниках сложнее, чем в диэлектриках и металлах, т. к. для них существенны и lэ, и lреш, а также в связи со значит. влиянием на l примесей, процессов биполярной диффузии, переноса экситонов и др. факторов. Влияние р на l тв. тел с хорошей точностью выражается линейной зависимостью l от р, причём у мн. металлов и минералов Я растёт с ростом р.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ТЕПЛОПРОВОДНОСТЬ
-
-один из видов переноса теплоты от более нагретых частей тела к менее нагретым, приводящий к выравниванию темп-ры. При Т. перенос энергии осуществляется в результате непосредств. передачи энергии от частиц (молекул, атомов, электронов), обладающих большей энергией, частицам с меньшей энергией. Если относит. изменение темп е ры Т на расстоянии ср. длины свободного пробега частиц l мало, то выполняется осн. закон Т. (закон Фурье): плотность теплового потока q пропорц. градиенту темп-ры:

где l -коэф. Т., или просто Т., не зависит от grad Т(l зависит от агрегатного состояния вещества, его атомно-молекулярного строения, темп-ры, давления, состава и т. д.).
Отклонения от закона Фурье могут появиться при очень больших значениях grad Т (напр., в сильных ударных волнах), при низких температурах (для жидкого Не II) и при темп-pax ~ 104- 105 К, когда в газах перенос энергии осуществляется не только в результате межатомных столкновений, но в осн. за счёт излучения (лучистая Т.). В разреженных газах, когда l сравнимо с расстоянием L между стенками, ограничивающими объём газа, молекулы чаще сталкиваются со стенками, чем между собой. При этом нарушается условие применимости закона Фурье и само понятие локальной темп-ры газа теряет смысл. В этом случае рассматривают не процесс Т. в газе, а. теплообмен между телами, находящимися в газовой среде. Процесс Т. в сплошной среде описывается теплопроводности уравнением.
Для идеального газа, состоящего из твёрдых сферич. молекул диаметром d, согласно кинетической теории газов, справедливо след. выражение для l (при d<<l<<L):

где r - плотность газа. cV - теплоёмкость единицы массы газа при пост, о б ъёме V,
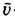 - ср. скорость движения молекул. Поскольку l пропорц. 1 /p, a r~p (p - давление газа), то Т. такого газа не зависит от р.
- ср. скорость движения молекул. Поскольку l пропорц. 1 /p, a r~p (p - давление газа), то Т. такого газа не зависит от р.
Кроме того, коэффициенты Т. l и вязкостиh связаны соотношением l = (5/2)hcV. В случае газа, состоящего из многоатомных молекул, существенный вклад в l вносят внутр. степени свободы молекул, что учитывает соотношение
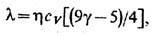
где g = с p/с V, с p - уд. теплоёмкость при пост. р. В реальных газах Т.-довольно сложная ф-ция Т и р, причём с ростом Т и p значение l возрастает. Для газовых смесей l может быть как больше, так и меньше l компонентов смеси, т. е. Т.- нелинейная ф-ция состава.
В плотных газах и жидкостях ср. расстояние между молекулами сравнимо с размерами самих молекул, а кине-тич. энергия движения молекул того же порядка, что и по-тенц. энергия межмолекулярного взаимодействия, В связи с этим перенос энергии столкновениями происходит значительно интенсивнее, чем в разреженных газах и скорость передачи энергии молекул от горячих изотермич. слоев жидкости к более холодным близка к скорости распространения малых возмущений р, равной скорости звука, т. е.
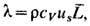 где us -скорость звука в жидкости,
где us -скорость звука в жидкости, 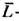 -ср. расстояние между молекулами. Эта ф-ла лучше всего выполняется для одноатомных жидкостей. Как правило, l жидкостей убывает с ростом Т и слабо возрастает с ростом р. В окрестностях критич. точек жидкостей перенос теплоты определяется кооперативными эффектами (см. Критические явления )и Т. с приближением к критич. точкам расходится как | Т-T к|-f, где
-ср. расстояние между молекулами. Эта ф-ла лучше всего выполняется для одноатомных жидкостей. Как правило, l жидкостей убывает с ростом Т и слабо возрастает с ростом р. В окрестностях критич. точек жидкостей перенос теплоты определяется кооперативными эффектами (см. Критические явления )и Т. с приближением к критич. точкам расходится как | Т-T к|-f, где 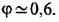
Т. твёрдых тел имеет разл. природу в зависимости от типа твёрдого тела. В диэлектриках, не имеющих свободных злектрич. зарядов, перенос энергии теплового движения осуществляется фононами. У твёрдых диэлектриков
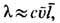 где с- теплоёмкость диэлектрика, совпадающая с теплоёмкостью газа фононов,
где с- теплоёмкость диэлектрика, совпадающая с теплоёмкостью газа фононов,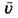 -ср. скоpость фононов, приблизительно равная скорости звука,
-ср. скоpость фононов, приблизительно равная скорости звука, 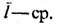 длина свободного пробега фононов. Существование определённого конечного значения
длина свободного пробега фононов. Существование определённого конечного значения 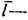 следствие рассеяния фононов на фононах (т. н. переброса процессы и нормальное рассеяние), на дефектах кристаллич. решётки (в частности, на границах кристаллитов и образца). Температурная зависимость l определяется зависимостью от темп-ры с и
следствие рассеяния фононов на фононах (т. н. переброса процессы и нормальное рассеяние), на дефектах кристаллич. решётки (в частности, на границах кристаллитов и образца). Температурная зависимость l определяется зависимостью от темп-ры с и 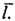
Т. металлов определяется движением и взаимодействием: носителей тока - электронов проводимости. В общем случае для металла l = l э+l реш, где l реш и l э - решёточная фононная и электронная составляющие, причём при обычных темп-pax, как правило,
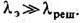 В процессе Т. каждый электрон переносит энергию kТ, благодаря чему отношение l э к электрич. проводимости s в широком интервале темп-р пропорц. Т (Видемана-Франца закон):
В процессе Т. каждый электрон переносит энергию kТ, благодаря чему отношение l э к электрич. проводимости s в широком интервале темп-р пропорц. Т (Видемана-Франца закон):
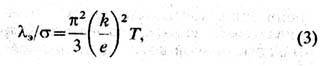
где е - заряд электрона. В связи с тем, что у большинства металловl реш <<l э в ур-нии (3) можно с хорошей точностью заменять l э на l. Обнаруженные отклонения от равенства (3) нашли своё объяснение в неупругости столкновений электронов, У полуметаллов Bi и Sb l решi сравнима с l э, что связано с малостью числа свободных электронов в них.
Явление переноса теплоты в полупроводниках сложнее, чем в диэлектриках и металлах, т. к. для них существенны и l э и l реш, а также в связи со значит. влиянием на l примесей, процессов биполярной диффузии, переноса экситонов и. др. факторов.
Влияние р на l твёрдых тел с хорошей точностью выражается линейной зависимостью l от р, причём у мн. металлов и минералов l растёт с ростом р.
Лит.: Гиршфельдер Дж., Кертисс Ч., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 1961; Зельдович Я. Б., Райзер Ю. П., Физика ударных волн и высокотемпературных гидродинамических явлений, 2 изд., М., 1966; Ашк-рофт Н., Мермин Н., Физика твердого тела, пер. с англ., т. 1-2, М-, 1979; Берман Р., Теплопроводность твердых тел, пер. с англ., М., 1979, С. П. Малышенко.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.