Akademik

- векторные частицы, за счёт обмена к-рыми осуществляется слабое взаимодействие. Они наз. "промежуточными" по историч. 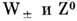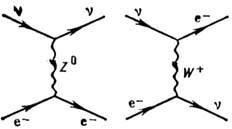причинам, поскольку их существование было предсказано теоретически задолго до их прямого обнаружения как реальных частиц (1983), а именно, локальное четырёхфермионное взаимодействие между заряженными токами и нейтральными тиками представлялось как результат "промежуточного" обмена виртуальными частицами [на рис. в ка-

честве примера показано, как указанный обмен осуществляется в рассеянии нейтрино 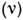на электроне

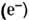]. Эти бозоны являются промежуточными в том же смысле, что и фотон (g) в рассеянии заряж. частиц. Обмен векторными бозонами 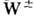(электрич. заряд соответственно + е и - е), 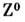(электрич. заряд 0) и g осуществляет связь между токами в единой теории электрослабого взаимодействия, основанной на группе симметрии SU(2)xU(l). В этой теории массы 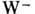(массы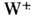

и 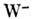равны) и 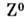-бозонов вычисляются теоретически и выражаются через константу Ферми 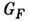и Вайнберга угол :

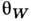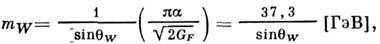
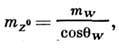
где a=1/137 - постоянная тонкой структуры. Угол Вайнберга и массы 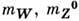измеряются в независимых

экспериментах, поэтому справедливость приведённых соотношений с процентной погрешностью служит очень важным аргументом в пользу теории электрослабого взаимодействия.

Масса (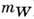) и ширина 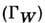заряж. W-бозона равны соответственно 80,6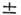0,4 ГэВ и 2,25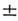0,14 ГэВ, масса 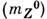и ширина 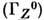нейтрального 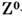-бозона равны 91,161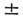0,031 ГэВ и 2,534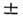0,027 ГэВ. Заряж. W-бозон в 70% случаев распадается в адронные состояния, в 30% - в лептонные состояния 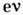, 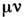и 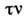(относительная вероятность каждой лептонной моды равна 10%). Z°-бозон распадается в адронные состояния в 71% случаев, его лептонные моды распада и их относительные вероятности равны соответственно: 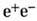(3,2%), 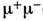(3,36%), 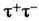(3,33%) и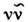

(19,2%). М. В. Терентъев.