Akademik

- теорема термодинамики неравновесных процессов, согласно к-рой при данных внеш. условиях, препятствующих достижению системой равновесного состояния, стационарному (неравновесному, но неизменному во времени) состоянию соответствует минимум производства энтропии. Если таких препятствий нет, то производство энтропии достигает своего абс. минимума - нуля. Доказана И. Р. Приго-жиным (I. R. Prigogine) в 1947 из соотношений взаимности Онсагера (см. Онсагера теорема). П. т. эквивалентна доказанному Онсагером (1931) принципу наим. рассеяния энергии и справедлива, если кинетич. коэф. в соотношениях Онсагера постоянны. Для реальных систем П. т. справедлива лишь приближённо, поэтому минимальность производства энтропии для стационарного состояния не является столь общим принципом, как максимальность энтропии для равновесного состояния (см. Второе начало термодинамики).

Производство энтропии в неравновесной термодинамич. системе, к-рая описывается n независимыми термодинамич. силами 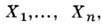равно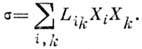

Если термодинамич. силы 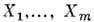постоянны, то минимум 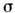соответствует условию 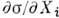= 0 при i= m + 1, ..., n, откуда поток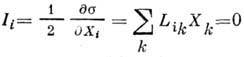

(при i = т+ 1, ..., n), т. е. все потоки, кроме тех, к-рые поддерживаются постоянными, равны нулю. Справедливо и обратное утверждение: в стационарном состоянии 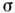минимально, поскольку.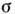- положительно определённая квадратичная форма.

В общем случае для непрерывной системы потоки и силы переменны в пространстве, т. е. зависят от точки 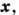и нужно рассматривать полное производство энтропии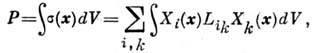

где интегрирование ведётся по объёму V системы, 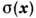- локальное производство энтропии. П. т. утверждает, что в стационарном состоянии функционал P минимален относительно вариации 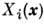при постоянных 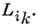Если 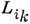не постоянны, то минимальность не имеет места. В общем случае P можно исследовать для нек-рых моделей. Напр., для системы, находящейся в контакте с термостатом и состоящей из невзаимодействующих частиц, каждая из к-рых может находиться в одном из двух энергетич. состояний, а также поглощать и испускать монохроматич. излучение, показано, что даже для далёких от равновесия состояний производство энтропии может очень мало отличаться от равновесного.

Лит. см. при ст. Термодинамика неравновесных процессов.

Д. Н. Зубарев.