- ПОГРАНИЧНЫЙ СЛОЙ
-
область течения вязкой жидкости (газа) с малой по сравнению с продольными размерами поперечной толщиной, образующаяся у поверхности обтекаемого тв. тела, у стен канала, по к-рому течёт жидкость, или на границе раздела двух потоков жидкости с разл. скоростями, темп-рами или хим. составом. П. с. характеризуется резким изменением в поперечном направлении скорости (динамич. П. с.) или темп-ры (тепловой, или температурный, П. с.) или же концентраций отд. хим. компонентов (диффузионный, или концентрационный, П. с.). На, формирование течения в П. с. осн. влияние оказывают вязкость, теплопроводность и диффузионная способность жидкости (газа). Внутри динамич. П. с. происходит плавное изменение скорости от её значения во внеш. потоке до нуля на стенке (вследствие прилипания вязкой жидкости к тв. поверхности). Аналогично внутри П. с. плавно изменяются темп-pa и концентрация.Режим течения в динамич. П. с. зависит от Рейнольдса числа Re и может быть ламинарным или турбулентным. При ламинарном режиме отд. ч-цы жидкости (газа) движутся по траекториям, форма к-рых близка к форме обтекаемого тела или условной границы раздела между двумя жидкими (газообразными) средами. При турбулентном режиме в П. с. на нек-рое осреднённое движение ч-ц жидкости в направлении осн. потока налагается хаотическое, пульсационное движение отд. жидких конгломератов. В результате интенсивность переноса кол-ва движения, а также процессов тепло- и массопереноса резко увеличивается, что приводит к возрастанию коэфф. поверхностного трения, тепло- и массообмена. Значение критич. числа Рейнольдса, при к-ром в П. с. происходит переход ламинарного течения в турбулентное, зависит от степени шероховатости обтекаемой поверхности, уровня турбулентности внеш. потока, Маха числа М и нек-рых др. факторов. При этом переход ламинарного режима течения в турбулентный с возрастанием Re происходит в П. с. не внезапно, а имеется переходная область, где попеременно чередуются ламинарный и турбулентный режимы.Толщина d динамич. П. с. определяется как то расстояние от поверхности тела (или от границы раздела жидкостей), на к-ром скорость в П. с. можно практически считать равной скорости во внеш. потоке. Значение 6 зависит гл. обр. от числа Рейнольдса, причём при ламинарном режиме течения d=l•Re-0,5, а при турбулентном — d=l•Re-0,2, где l — характерный размер тела.Развитие теплового П. с. определяется, помимо числа Рейнольдса, также Прандтля числом, к-рое характеризует соотношение между толщинами динамич. и теплового П. с. Соответственно на развитие диффузионного П. с. дополнит. влияние оказывает диффузионное число Прандтля или Шмидта число.Внутри П. с. кинетич. энергия молекул переходит в тепловую, вследствие чего при больших скоростях внеш. потока локальная темп-pa газа увеличивается. В случае теплоизолированной поверхности темп-pa газа в П. с. может приближаться к т. н. темп-ре торможения Т0=Те(1+((k-1)/2)М2), где Те— темп-pa газа вне П. с., k=cp/cv— отношение теплоёмкостей при пост. давлении и пост. объёме.Характер течения в П. с. оказывает решающее влияние на отрыв потока от поверхности обтекаемого тела. Причина этого заключается в том, что при наличии достаточно большого положит. продольного градиента давления кинетич. энергия заторможённых в П. с. ч-ц жидкости становится недостаточной для преодоления сил давления, течение в П. с. теряет устойчивость и возникает т. н. отрыв потока (см. ОТРЫВНОЕ ТЕЧЕНИЕ).При больших числах Рейнольдса толщина П. с. очень мала по сравнению с характерными размерами тела. Поэтому почти во всей области течения, за исключением тонкого П. с., влияние сил вязкости несущественно по сравнению с инерционными силами, и жидкость в этой области можно рассматривать как идеальную. Одновременно вследствие малой толщины П. с. давление в нём в поперечном направлении можно практически считать постоянным. В результате весьма эффективным оказывается такой метод изучения обтекания тел потоком жидкости (газа), когда всё поле течения разбивается на две части — область течения идеальной жидкости и тонкий П. с. у поверхности тела. Течение в первой области изучается с помощью ур-ний движения идеальной жидкости, что позволяет определить распределение давления вдоль поверхности тела; тем самым определяется и давление в П. с. Течение внутри П. с. рассчитывается после этого с учётом вязкости, теплопроводности и диффузии, что позволяет определить поверхностное трение и коэфф. тепло- и массообмена. Однако такой подход оказывается неприменимым в явном виде в случае отрыва потока от поверхности тела. Он неприменим и при малых Re, когда влияние вязкости распространяется на довольно большую часть возмущённой области течения.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- ПОГРАНИЧНЫЙ СЛОЙ
-
- область течениявязкой жидкости (газа) с малой по сравнению с продольными размерами поперечнойтолщиной, появляющаяся у поверхности обтекаемого твёрдого тела или у границыраздела двух потоков жидкости с разл. скоростями, темп-рамп или хим. составом. Возникновение П. с. связано с явлением переноса в жидкости кол-ва движения, теплоты и массы, характеризуемых коэф. вязкости, теплопроводности и диффузии. Образование и развитие П. с. можно проследить на примере динамического(скоростного) П. с. у поверхности
тела, обтекаемого потоком жидкостп илигаза (рис. 1). Вследствие вязкости жидкости она "прилипает" к поверхноститела, т. е. на стенке продольная составляющая скорости жидкости раина нулю(если поверхность тела непроницаемая, то здесь равна пулю и поперечнаясоставляющая скорости). Разрыв продольной составляющей скорости в вязкойжидкости существовать не может, поэтому возникает переходная область течения, т. е. П. с., в к-ром происходит плавное изменение скорости от нуля на стенкедо нек-рого конечного значения во внеш. потоке, где влияние вязкости исчезает.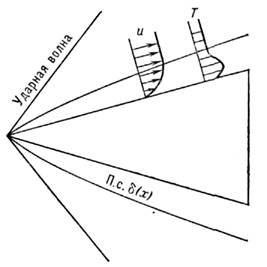
Рис. 1. Профили скорости и температурыв пограничном слое на поверхности острого конуса в сверхзвуковом потокегаза.
Толщина такой переходной области и профильскорости в ней определяются ур-ниями сохранения кол-ва движения. Помимодпнамич. П. с. при обтекании тела можно выделить также тепловой (температурный)П. с., образующийся в случае несовпадения темп-ры поверхности тела и темп-рыжидкости, а также концентрационный (диффузионный) П. с., образующийся припротекании на стенке хим. реакции или же при вдуве инородного газа черезпроницаемую поверхность тела. В тепловом П. с. темп-pa жидкости непосредственноу стенки равна темп-ре поверхности тела. Если тело обтекается жидкостьюс малой скоростью, то внутри теплового П. с. происходит монотонное изменениетемп-ры жидкости от темп-ры поверхности до темп-ры внеш. потока. Если жетело обтекается сверхзвуковым потоком газа, то внутри теплового П. с. вследствиеторможения газа и перехода кинетич. энергии во внутр. энергию молекул можетвозникать максимум темп-ры.
Другой часто встречающийся на практикеслучай П. с. - это слой смешения, образующийся у границы струп, истекающейиз сопла, напр. летат. аппарата с воздушно-реактивным или ракетным двигателем(рис. 2). В слое смешения скорость газа изменяется от скорости полёта доскорости истечения продуктов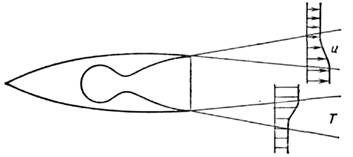
Рис. 2. Слой смешения при истечении струииз сопла ракеты при полёте в атмосфере.
сгорания из сопла (в системе координат, связанной с летат. аппаратом), а темп-pa - от темп-ры атмосферы до темп-рыпродуктов сгорания. Так же плавно изменяются концентрации компонент внеш. среды и продуктов сгорания.
Толщина дпнамич. П. с. определяется критериемРейнольдса (см. Рейнольдса число Re), к-рый характеризует соотношениемежду инерц. силами и силами внутр. трения. Чем больше Re, тем меньшетолщина П. с. по сравнению с характерным размером тела. Обычно число Re намного превышает единицу, так что толщина П. с.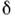 мала по сравнению с размерами тела. Кроме того, при этом оказывается несущественнымизменение давления поперёк ГГ. с. В результате параметры жидкости или газана впеш. границе П. с. могут быть определены так, как будто тело обтекаетсяпотоком идеальной (невязкой) жидкости. В более строгой постановке следуетрассматривать обтекание идеальной жидкостью нек-рого эфф. тела, увеличенногона т. н. толщину вытеснения П. с. Это позволяет упростить методы расчётатрения и теплообмена между телом и обтекающей его жидкостью (газом). Дляэтого поток подразделяют на две части - область течения идеальной жидкостии тонкий П. с. у поверхности тела. Решая задачу об обтекании тела невязкнмпотоком, находят распределение давления вдоль поверхности тела, а тем самыми давление в П. с. Течение внутри П. с. рассчитывается после этого с учётомвязкости, теплопроводности и диффузии, что позволяет определить силы поверхностноготрения и коэф. тепло- и массообмена.
мала по сравнению с размерами тела. Кроме того, при этом оказывается несущественнымизменение давления поперёк ГГ. с. В результате параметры жидкости или газана впеш. границе П. с. могут быть определены так, как будто тело обтекаетсяпотоком идеальной (невязкой) жидкости. В более строгой постановке следуетрассматривать обтекание идеальной жидкостью нек-рого эфф. тела, увеличенногона т. н. толщину вытеснения П. с. Это позволяет упростить методы расчётатрения и теплообмена между телом и обтекающей его жидкостью (газом). Дляэтого поток подразделяют на две части - область течения идеальной жидкостии тонкий П. с. у поверхности тела. Решая задачу об обтекании тела невязкнмпотоком, находят распределение давления вдоль поверхности тела, а тем самыми давление в П. с. Течение внутри П. с. рассчитывается после этого с учётомвязкости, теплопроводности и диффузии, что позволяет определить силы поверхностноготрения и коэф. тепло- и массообмена.
Соотношение между толщинами динамич. итеплового П. с. определяется Прапдтля числом Рr, а соотношение междутолщинами динамич. и концентрац. П. с. - Шмидта числом Sc. Для воды, воздуха и мн. др. непроводящих жидкостей и газов числа Рr и Sc близки к 1, вследствие чего толщины динамич., теплового и концентрац. П. с. близки между собой.
Наличие вынужденного течения жидкостиили газа не является обязательным для образования П. с. у поверхности тела. Примером является П. с., образующийся у поверхности погружённого в жидкостьтела или у стенок сосуда с жидкостью в случае свободной конвекции, возникающейпри наличии разности темп-р жидкости и твёрдой стенки (рис. 3). В этомслучае толщина П. с. определяется Грасгофа числом Gr.
Рис. 3. Пограничный слой на стенках сосудас жидкостью при подводе тепла сбоку.
Характер течения жидкости внутри П. с. показывает, что при достаточно больших размерах тела (а точнее, при достаточнобольших числах Re или Gr, рассчитываемых по длине тела) существуютдва режима течения - ламинарное и турбулентное.
Ламинарный П. с. В нач. части П. с. течение является ламинарным, упорядоченным. Отд. частицы жидкости движутсяпо плавным траекториям, не пересекаясь и не перемешиваясь друг с другом. Форма этих траекторий близка к форме обтекаемого тела.
Днфференц. ур-ния течения вязкого теплопроводногооднородного газа в ламинарном П. с. у поверхности тела произвольной формымогут быть получены нз Навье - Стакса уравнений, отбрасыванием членов, к-рые несущественны при достаточно больших числах Рейнольдса, когда толщинаП. с. мала по сравнению с размерами тела. Основы такого подхода были заложеныЛ. Прандтлем (L. Prandtl) в 1904. В случае стационарного двумерного теченияэти упрощённые ур-ния На-вье - Стокса, известные как yp-ния П. с., илиур-ния Прандтля, представляют собой нелинейные днфференц. yp-ния параболич. типа и имеют вид: ур-нпе сохранения количества движения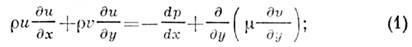
ур-ние сохранения энергии
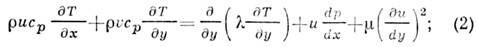
ур-ние неразрывности
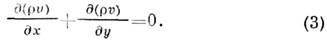
Здесь х и y - координаты, направленные вдоль поверхности тела и по нормали к ней, и и v- составляющие скорости вдоль этих координат,
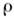 - плотность, р - давление,
- плотность, р - давление,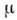 - козф. дпнамич. вязкости, Т - темп-pa, c р- уд. теплоёмкость при пост. давлении,
- козф. дпнамич. вязкости, Т - темп-pa, c р- уд. теплоёмкость при пост. давлении,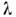 - коэф. теплопроводности.
- коэф. теплопроводности.
Граничные условия к системе ур-ний (1)- (3) имеют вид: при y = 0 величины и =0, v = vw,Т = Tw; при y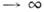 и
и 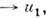 Т
Т  T1.
T1.
В случае смеси газов, в к-рой могут протекатьхим. реакции, к ур-ниям (1) - (3) добавляются ур-ния неразрывности дляотд. компонент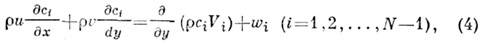
а ур-ние сохранения энергии удобнее записыватьчерез энтальпию Н газа

где с i- массовая концентрация i-й компоненты, Vi - скорость диффузии,wi- массовая скорость образования i -й компоненты в единице объёмав результате хим. реакций, Н i- энтальпия i -йкомпоненты и
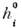 - теплота образования i -й компоненты при стандартных условиях. Скоростьдиффузии определяется градиентами концентраций отд. компонент (концентрац. диффузия), а также градиентом темп-ры (термодиффузия).
- теплота образования i -й компоненты при стандартных условиях. Скоростьдиффузии определяется градиентами концентраций отд. компонент (концентрац. диффузия), а также градиентом темп-ры (термодиффузия).
Для решения ур-ний П. с. используютсяразл. методы, среди к-рых можно выделить две осн. группы - численные (конечно-разностные)и интегральные. Первая группа методов основана на численном интегрированииисходных ур-ний П. с. методом сеток, или конечных разностей. Совр. ЭВМпозволяют это делать практически без внесения существенных упрощающих предположений, с учётом всех особенностей геометрии, физ.-хим. процессов и т. п. Широкоераспространение в численных расчётах получил анализ ур-ний П. с. для разл. частных случаев, когда, вводя спец. переменные и опуская нек-рые несущественныечлены, с одной стороны, получают упрощение исходной системы ур-ний, а сдругой - сами результаты получаются в более обобщённом виде. К ним относятсяразл. автомодельные решения, для к-рых имеет место понижение размерностизадачи (напр., случаи П. с. на плоской пластине и конусе, в окрестностикритич. точки затупленного тела, на клиновидных телах в дозвуковом потоке).См. Автомодельное течение.
Вторая группа методов основана на использованииур-нпй П. с. в интегральной форме. В этих ур-ниях в качестве зависимыхпеременных выступают нек-рые интегральные характеристики П. с.: толщинавытеснения
толщина потери импульса
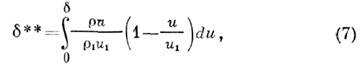
толщина потери энергии
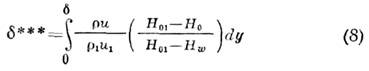
(индексы "1" относятся к внеш. потоку,"01" - к границе П. с., "О" - к П. с., а "w" - к обтекаемой поверхности).Интегральные ур-ния П. с. получаются из дифференц. ур-ний типа (1) - (5)интегрированием последних по поперечной координате от 0 до внеш. границыП. с.
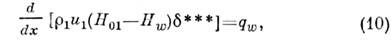
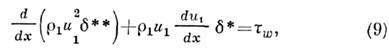
где
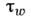 - напряжение трения на поверхности тела, а
- напряжение трения на поверхности тела, а 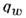 - тепловой поток через его поверхность. Интегральные ур-ния позволяют учестьизменяющиеся условия течения вверх по потоку от рассматриваемой точки тела. Для решения интегральных ур-ний П. с. (9) - (10) необходимо иметь сведенияо профилях скорости и энтальпии (или темп-ры) внутри П. с. В основе разл. приближённых методов решения ур-ний П. с. лежит использование нек-рых наборовпрофилей скоростей и темп-р внутри П. с., напр. степенные профили. Знаниепрофилей скорости и темп-ры позволяет связать между собой разл. характерныетолщины П. с., входящие в ур-ния (9) - (10).
- тепловой поток через его поверхность. Интегральные ур-ния позволяют учестьизменяющиеся условия течения вверх по потоку от рассматриваемой точки тела. Для решения интегральных ур-ний П. с. (9) - (10) необходимо иметь сведенияо профилях скорости и энтальпии (или темп-ры) внутри П. с. В основе разл. приближённых методов решения ур-ний П. с. лежит использование нек-рых наборовпрофилей скоростей и темп-р внутри П. с., напр. степенные профили. Знаниепрофилей скорости и темп-ры позволяет связать между собой разл. характерныетолщины П. с., входящие в ур-ния (9) - (10).Турбулентный П. с. По мере увеличениярасстояния вдоль поверхности тела местное число Рейнольдса возрастает иначинает проявляться неустойчивость ламинарного течения по отношению кмалым возмущениям. Такими возмущениями могут служить пульсации скоростиво внеш. набегающем потоке, шероховатость поверхности и др. факторы. Врезультате ламинарная форма течения переходит в турбулентную, при этомна главное "осреднённое" движение жидкости или газа в продольном направлениинакладываются хаотич., пульсац. движения отд. жидких конгломератов в поперечномнаправлении. В результате происходит интенсивное перемешивание жидкости, вследствие чего интенсивность переноса в поперечном направлении кол-вадвижения, теплоты и массы резко увеличиваются. Потеря устойчивости и переходк турбулентному режиму течения внутри П. с. происходят при нек-ром характерномчисле Рейнольдса, к-рое наз. критическим. Величина Re кр зависит от мн. факторов - степени турбулентности набегающего потока, шероховатостиповерхности Маха числа М внеш. потока, относит. темп-ры поверхности, вдува или отсоса вещества через поверхность тела и др. Поскольку переходламинарного режима течения в турбулентный связан с потерей устойчивости, то сам этот процесс не является достаточно стабильным, вследствие чегоимеет место "перемежаемость" режима течения в пределах нек-рой области, к-рую называют областью перехода.
Изменение режима течения в П. с. сопровождаетсяутолщением слоя и деформацией профилей скорости, темп-ры и концентраций. Одновременно возрастают коэф. поверхностного трения, тепло- и массообмена, а также изменяется характер их распределения вдоль поверхности тела (рис.4).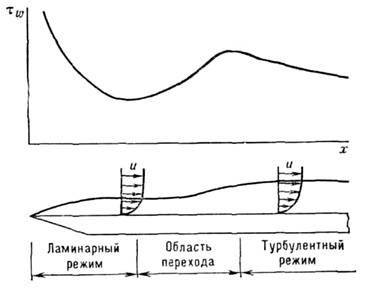
Рис. 4. Изменение режима течения в пограничномслое и поверхностного трения на плоской пластине.
Течение внутри турбулентного П. с. носитпульсационный, хаотич. характер: давление, плотность, скорость, темп-pa,концентрации и др. характеристики поля течения быстро изменяются, пульсируют, и притом хаотически. В этом случае при матем. описании течения каждый параметрможно представить в виде суммы осредпённого по времени, или среднего, значенияи пульсационного. Напр.,
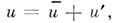 Т=
Т=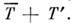 Интегралпо времени от пульсац. составляющей любого параметра за достаточно большойинтервал времени
Интегралпо времени от пульсац. составляющей любого параметра за достаточно большойинтервал времени 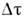 (строго говоря, при
(строго говоря, при 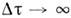 )равен нулю
)равен нулю 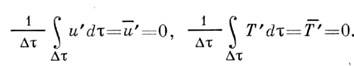
Однако осреднённые значения произведенийпульсац. составляющих разл. параметров могут и не обращаться в нуль, чтосвидетельствует о корреляции между пульсациями. Именно корреляция междупульсациями разл. параметров объясняет нек-рый дополнит. механизм передачикол-ва движения, энергии и диффузии в поперечном направлении.
Дифференц. ур-ния турбулентного П. с. имеют тот же вид, что и ур-ния ламинарного П. с. (1) - (5), с той лишьпоправкой, что входящие в эти ур-ния коэф. вязкости, теплопроводности идиффузии представляются в виде суммы молекулярной и турбулентной составляющих. Вследствие наличия в этих ур-нпях турбулентных коэф. переноса вся системаур-ний турбулентного П. с. оказывается незамкнутой. Поэтому для полученияприближённых решений ур-нпй турбулентного П. с. привлекаются дополнит. гипотезы и допущения. В частности, весьма плодотворной оказалась предложеннаяЛ. Прандтлем гипотеза "пути перемешивания" l, позволяющая выразитькоэф. турбулентной вязкостп через ср. плотность и градиент ср. скорости

С помощью аналогичных выражений могут бытьпредставлены также коэф. турбулентной теплопроводности и коэф. турбулентнойдиффузии.
В общем случае турбулентный П. с. можнопо высоте разделить на 3 области (рис. 5): пристеночный ламинарный подслой, где турбулентные пульсации затухаюти решающую роль играют молекулярныевязкость и теплопроводность; турбулентное ядро, в к-ром турбулентные вязкостьи теплопроводность существенно превышают соответствующие молекулярные переносныесвойства, и промежуточную переходную область. В результате многочисленныхэксперпм. исследований установлено, что распределение скорости внутри турбулентногоядра описывается нек-рым универсальным эмпирич. законом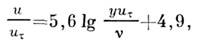
где
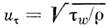 - т. н. скорость сдвига, или динамич. скорость, а
- т. н. скорость сдвига, или динамич. скорость, а 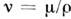 - кинематич. вязкость. Следует отметить, что логарифмич. закон распределенияскорости внутри турбулентного ядра П. с. может быть получен исходя из ф-лыПрандтля для турбулентной вязкости (11) в предположении, что входящий вэту ф-лу путь перемешивания l пропорц. расстоянию от стенки. Припостроении приближённых методов расчёта турбулентного П. с. широко используютсятакже степенные профили скорости и темп-ры
- кинематич. вязкость. Следует отметить, что логарифмич. закон распределенияскорости внутри турбулентного ядра П. с. может быть получен исходя из ф-лыПрандтля для турбулентной вязкости (11) в предположении, что входящий вэту ф-лу путь перемешивания l пропорц. расстоянию от стенки. Припостроении приближённых методов расчёта турбулентного П. с. широко используютсятакже степенные профили скорости и темп-ры 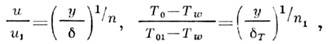
где Т0, Т01 и Tw - соответствующие темп-ры торможения в П. с.,на границе П. с. и стенки. Значения показателей степени для дозвуковыхскоростей изменяются от 1/7 до 1/9 при увеличении числа Рейнольдса и несущественно возрастают при большихчислах Маха. В прикладных расчётах трения, тепло- и массообмена в турбулентномП. с. наиб. распространение получили полуэмпирич. методы, в частности метод, основанный на эксперим. данных по турбулентному трению на плоской пластине(аналогия процессов тепломассообмена и трения и введение понятия "эффективнойдлины"). Эксперпм. данные по турбулентному коэф. трения на плоской пластине, обтекаемой сверхзвуковым потоком, могут быть представлены аппроксимационнойф-лой
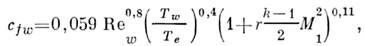
где
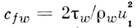 - коэф. поверхностного трения,
- коэф. поверхностного трения,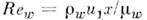 - число Рейнольдса, Т е = Т1(1 + r(k -1) М 2/2) - равновесная темп-pa стенки,r- коэф. восстановления темп-ры, М1 - числоМаха внеш. потока, k = с р/с V- отношение теплоёмкостейпри пост. давлении и пост. объёме.
- число Рейнольдса, Т е = Т1(1 + r(k -1) М 2/2) - равновесная темп-pa стенки,r- коэф. восстановления темп-ры, М1 - числоМаха внеш. потока, k = с р/с V- отношение теплоёмкостейпри пост. давлении и пост. объёме.Предположение об аналогии процессов тепломассообменаи трения, следующее из самого вида ур-ний П. с., позволяет для безразмерногокоэф. теплообмена на пластине - Нуссельта числа Nu - записать ф-лу, к-рая хорошо согласуется с имеющимися эксперим. данными:
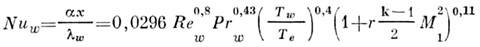
(
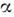 - коэф. теплоотдачи,
- коэф. теплоотдачи,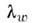 - коэф. теплопроводности газа на стенке). Для переноса этой зависимостина случай П. с. на теле произвольной формы может быть использован предложенныйВ. С. Авдуевским метод "эффективной длины", предполагающий, что тепловойпоток в рассматриваемой точке тела будет таким же, как в нек-рой точкена пластине при одинаковых местных параметрах течения и при условии, чтов рассматриваемых точках тела и пластины толщины потери энергии
- коэф. теплопроводности газа на стенке). Для переноса этой зависимостина случай П. с. на теле произвольной формы может быть использован предложенныйВ. С. Авдуевским метод "эффективной длины", предполагающий, что тепловойпоток в рассматриваемой точке тела будет таким же, как в нек-рой точкена пластине при одинаковых местных параметрах течения и при условии, чтов рассматриваемых точках тела и пластины толщины потери энергии  (8) также одинаковы. Т. о., задача теплообмена сводится к определению эфф. длины пластины, для к-рой достигается необходимое значение толщины потериэнергии. Если темп-pa стенки постоянна, то, напр., для осесимметричноготела при произвольном распределении давления вдоль поверхноста эфф. длина х эф равна
(8) также одинаковы. Т. о., задача теплообмена сводится к определению эфф. длины пластины, для к-рой достигается необходимое значение толщины потериэнергии. Если темп-pa стенки постоянна, то, напр., для осесимметричноготела при произвольном распределении давления вдоль поверхноста эфф. длина х эф равна 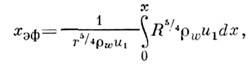
где R - переменный радиус поперечногосечения тела, a u1 - скорость жидкости или газа на внеш. границе П. с.
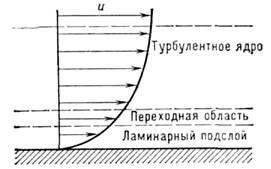
Рис. 5. Внутреннее строение турбулентногопограничного слоя.
Течение в П. с. оказывает решающее влияниена явление отрыва потока от поверхности обтекаемого тела как во внешних(напр., обтекание крыла), так и во внутренних (напр., течение в диффузоре)течениях. Отрыв происходит в результате совместного действия двух осн. факторов - торможения жидкости в П. с. и воздействия перепада давления. Внутрп П. с. скорость жидкости или газа уменьшается и её кинетич. энергииоказывается недостаточно для преодоления возрастающего давления. В результатевблизи поверхности возникает область возвратного течения, П. с. утолщаетсяи, наконец, осн. поток отрывается от стенки (рис. 6) (см. Отрывное течение).
Способность течения в П. с. противостоятьповышению давления имеет важное значение в случае падения на тело ударныхволн, или скачков уплотнения. Существует критич. значение отношениядавлений в скачке р 2/p1 (т. н. критич. перепад, где р 2 - давление за, а р 1- передскачком уплотнения), при к-ром взаимодействие скачка уплотнения с П. с. приводит к отрыву последнего.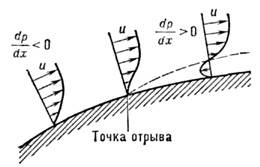
Рис. 6. Отрыв пограничного слоя при наличииположительного градиента давления.
Величина критич. перепада давления ( р 2/ р 1) кр зависит от режима течения в П. с., числа Маха, а для ламинарного П. с. и от числа Рейнольдса. При воздействии достаточно сильного скачка уплотненияна тело П. с. отрывается и возникает конфигурация т. н.
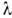 -скачка, у к-рого наклон передней "ножки" формируется таким образом, чтобы перепаддавления на ней был равен критическому (рис. 7).
-скачка, у к-рого наклон передней "ножки" формируется таким образом, чтобы перепаддавления на ней был равен критическому (рис. 7).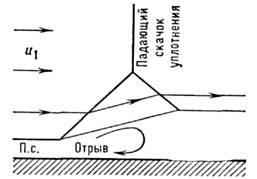
Рис. 7. Картина течения при взаимодействиипограничного слоя с действующим на тело скачком уплотнения.
Лит.: Лойцянский Л. Г., Механикажидкости и газа, 6 изд., М., 1987; его же, Ламинарный пограничный слой, М., 1962; Шлихтинг Г., Теория пограничного слоя, пер. с нем., М., 1974;Основы теплопередачи в авиационной и ракетно-космнческой технике, М., 1975.
Н. А. Анфимов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.