Akademik

- асимптотич. метод для описания дифракции коротких волн в системах, размеры к-рых dcущественно превышают длину волны l.К. уточняет геометрической оптики метод в окрестностях каустик н фокусов, в зонах полутени, при описании широких волновых пучков и т. п. Обособившись сначала в самостоят, раздел электродинамики, К. в дальнейшем приобрела универсальный характер как метод, пригодный для волн любой природы и в любом диапазоне, если только выполнен необходимый критерии её применимости: dдl.К. имеет дело с описанием волновых полей, характеризующихся разл. масштабами изменения комплексной лучевой амплитуды в направлении локального волнового вектора и в перпендикулярном направлении. В отличие от геом. оптики, описывающей распространение волн в каждой лучевой трубке независимо, К. учитывает эффекты поперечной диффузии лучевой амплитудыв смежные лучевые трубки, т. е. по фронтам распространяющихся волн.
Волновые пучки. Простейшей моделью К. является монохроматич. параксиальный волновой пучок в однородной среде, образуемый соседними зонами полутени при дифракции плоской волны на большом (в масштабе l) отверстии в непрозрачном экране (рис. 1). Такой пучок в случае скалярного поля можно описать ф-цией

u=А(х, у, z )ехp(-ikz+iwt),(1)

где медленная амплитуда А(х, у, z )меняется в масштабах l_^ дl по х, у и l_||=kl_||² дl_^ - по z, k=2p/l=w/с. Подстановка (1) в волновое ур-ние

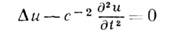
и пренебрежение членом Р ²A/ Р z², имеющим по отношению к др. слагаемым порядок (kl_^)^-2 Ъ1, приводят к параболич. ур-нию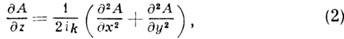

описывающему поперечную диффузию комплексной лучевой амплитуды. Ур-ние (2) сходно с ур-нием Шрёдингера в квантовой механике.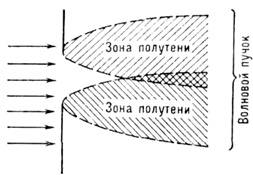

Рис. 1. Формирование волнового пучка при дифракции плоской волны на большом отверстии.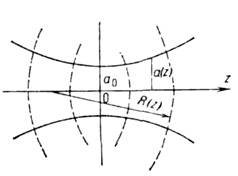

В теории эл.-магн. поля оно впервые было получено М. А. Леонтовичем в 1944 и носит его имя. Мнимость коэф. диффузии D=(2ik)^-1 в (2) означает, что диффузия амплитуды сопровождается изменением фазы (см. Леонтовича параболическое уравнение). Решение параболич. ур-ния (2), описывающее амплитуду А( х, у, z )по её значению А( х, у,0) в сечении z=0, можно представить в виде

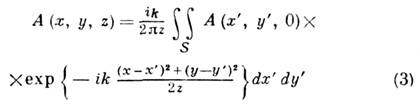
(дифракция Френеля).
Важным классом решений ур-ния (2) являются гауссовы пучки, моды к-рых имеют автомодельный характер, т. е. сохраняют с точностью до масштаба свою структуру в разных сечениях z=const. Осн. гауссов пучок (рис. 2) описывается ф-цией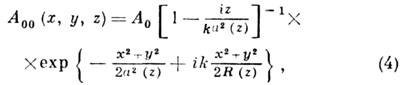

где А₀ - амплитуда пучка,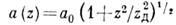 -радиус пучка, R(z)=-z-z _д²/z - радиус кривизны его фазового фронта, а ₀ - радиус пучка в сечении z=0. Величину z _д=ka₀² наз. дифракц. длиной пучка; на расстоянии z=z _д радиус пучка равен а ₀ Ц2, а радиус кривизны фазового фронта минимален: |R(z _д)|=2z _д. Геом. расходимость q _г=a(z)/|R(z)| и дифракц. расходимость q _д=l/ka(z) гауссова пучка нулевого порядка в сечении z образуют инвариантq² _п=q² _г+q² _д=(ka₀)^-2,равный полной расходимости пучка на бесконечности. При z<z _д в пучке преобладает дифракц. расходимость, а при z>z _д - геометрическая. Поперечная структура пучков высших порядков А_m,n( х, у, z )описывается произведением функций Эрмита соответствующих порядков. Радиусы этих пучков и их расходимости внаправлениях х и у в 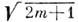и 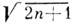раз больше, чем для осн. пучка. Особенностью осн. гауссова пучка является возможность представления его в виде сферич. волны, выходящей из комплексной точки и имеющей комплексную кривизну 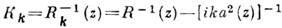. Изменение параметров гауссова пучка, описываемого ф-лой (4), эквивалентно при таком подходе уменьшению радиуса кривизны R_k сферич. волны на величину z: R_k(z)=R_k(0)-z. Сферич. волне сопоставляется матрица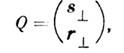

образованная вектором r_^( х, у )нек-рой точки на фронте волны и поперечной проекцией лучевого вектора s_^=-r_^/R_k в тoй же точке. Преобразование гауссова пучка оптич. системой с произвольной матрицей перехода (лучевой матрицей)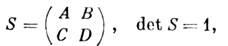

как и для сферич. волн, сводится к перемножению матриц S и Q.При этом выходной пучок описывается обычной ф-лой геом. оптики: K'_k=(К _k А-B)/(K_k С-D).
Квазиоптические системы. Практически важным классом являются периодич. квазиоптич. системы: открытые волноводы (лучеводы) и открытые резонаторы. Если S - матрица перехода такой системы, то её собств. волны определяются из решения ур-ния

условием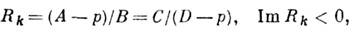

где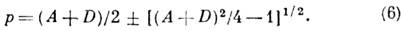

При |А+D|<2 собств. значения р комплексны, |р|=1 и собств. волнами волновода, согласно (6), являются гауссовы пучки. Это область устойчивости, в к-рой лучи в периодич. системе совершают финитное движение. При |A+D|>2 собственными являются сферич. нелокализованные волны. Это область неустойчивости, в к-рой движение лучей инфинитно: |p_l|<l, |p₂|>1. Примером лучевода может служить периодич. последовательность линз (линзовая линия, рис. 3)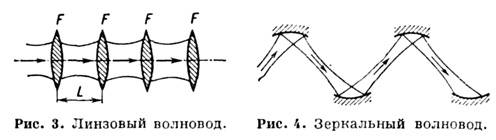

или эллиптич. зеркал (зеркальная линия, рис. 4), осуществляющих последоват. фазовую коррекцию пучка. Область устойчивости таких линий определяется условием (L/4)<F<:, где F - фокусное расстояние одного элемента линии, L - расстояние между ними. В открытых резонаторах (рис. 5) поле формируется волновыми пучками, многократноотражающимися от зеркал. Области устойчивости и структуры пучков в резонаторах со сферич. зеркалами определяются ур-нием (5), где под S в общем случае следует понимать лучевую матрицу, отвечающую полному обходу пучком резонатора (см. Оптический резонатор).

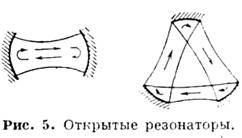
Квазиоптич. системы открытого типа заменили традиционные в диапазоне СВЧ объёмные резонаторы и волноводы металлические в диапазонах миллиметровых, субмиллиметровых и оптич. волн. Прежние системы оказались непригодными из-за повышения требований к точности изготовления элементов вследствие уменьшения их размеров, снижения электрич. прочности, значит, возрастания потерь в экранирующих проводниках. Использовать же экранированные системы с dдl (т. е. сверхразмерные волноводы и резонаторы) трудно вследствие уплотнения спектра собств. волновых чисел (волноводы) или собств. частот (резонаторы), практически сливающихся в сплошной спектр из-за уширения отд. линий. В открытых системах разрежение спектра (селекция мод) происходит из-за отсутствия боковых стенок, что не только ограничивает допустимый диапазон волновых векторов параксиальной областью, но и позволяет подбором размеров зеркал или диафрагм увеличивать потери на излучение (дифракц. потери) мод высших типов.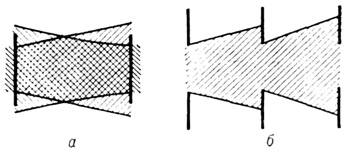

Рис. 6. Формирование волнового пучка в резонаторе с плоскими зеркалами (а) и в диафрагменной линии (б).

В квазиоптич. системах с огранич. корректорами гауссовы пучки уже не являются собств. модами, структура к-рых определяется теперь из решения ур-ния типа 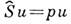с интегральным оператором 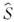, построенным аналогично (3) с учётом фазовой коррекции пучка зеркалами или линзами. Помимо геометрии корректоров в диафрагмиров. системах важную роль играет параметр N=a²/lL,равный квадрату отношения радиуса корректора к радиусу первой зоны Френеля. Этот параметр определяет степень ограничения пучков, а следовательно, и уровень дифракц. потерь. Дифракц. потери, слабо возмущающие структуру полей в открытых волноводах и резонаторах с фокусирующими элементами, полностью формируют её в резонаторах с плоскими зеркалами и эквивалентных им линиях, образованных периодич. последовательностью поглощающих диафрагм (рис. 6). В таких системах устанавливаются собств. структуры волновых пучков, убывающие к краю зеркала или диафрагмы, что приводит к снижению потерь на излучение. Параксиальные волновые пучки могут формироваться не только в свободном пространстве, но и в слабонеоднородных средах, напр, в рефракционных волноводах, используемых в технике (см. Волоконная оптика), и природных (ионосферные и атмосферные волноводы, подводный звуковой канал). Их описывают при помощи параболич. ур-ния

обобщающего ур-ние (2) на случай среды с перем. коэф. преломления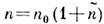 , где 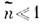. В частности, в волноводах с 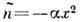( х - поперечная координата) собств. модами по-прежнему являются гауссовы пучки. Если коэф. преломления зависит от амплитуды поля, то параболич. ур-ния типа (7) применяют для описания волн в нелинейных средах (см., напр., Самофокусировка света).Квазиоптич. подход на основе ур-ния (7) можно развить и для описания квазимонохроматич. волновых пакетов в диспергирующих средах. На основе соответствующих решений геометрической оптики строится также К. сильно расходящихся пучков и полей около каустик. Лит.: Леонтович М. А., Об одном методе решения задач о распространении электромагнитных волн вдоль поверхности земли, "Изв. АН СССР. Сер. физ.", 1944, т. 8, с. 16; Малюжинец Г. Д., Развитие представлений о явлениях дифракции, "УФН", 1959, т. 69, с. 321; Квазиоптика, пер. с англ, и нем., М., 1966; Вайнштейн Л. А., Открытые резонаторы и открытые волноводы, М., 1966; Маркузе Д., Оптические волноводы, пер. с англ., М., 1974.С. Н. Власов, В. И. Таланов.