Akademik

        определяет переход от посылок к следствиям; более точно — устанавливает соответствие между некоторой совокупностью высказываний (формул), наз. посылками, и одним определ. высказыванием (формулой), наз. логич. следствием из этих посылок.

(п р а в и л о п р е о б р а з о в а н и я) – разрешение переходить от утверждений таких-то и таких-то видов, называемых посылками, к утверждению такого-то вида, наз. заключением. Напр., от утверждений вида "А" и "если А, то В" П. в., наз. modus ponens, разрешает перейти к утверждению вида "В". Аксиомы (а также схемы аксиом) можно рассматривать как П. в. из пустого (см. Пустое) множества посылок. П. в. делят на т.н. "правила прямого вывода" (п.п.в.) и "правила косвенного вывода" (п.к.в.). П.п.в. устанавливают, какие утверждения могут считаться выведенными из данных посылок: это, напр., утверждение, совпадающее с одной из посылок, совпадающее с одной из аксиом, полученно из ранее выведенных в данном рассуждении утверждений по к.-л. П.в. П.к.в. устанавливают, что если проведены такие и такие-то рассуждения, то может считаться проведенным и такое-то рассуждение. Примерами п.к.в. могут служить правила, лежащие в основе доказательств разбором случаев, доказательства от противного, теоремы о дедукции и др. При описании к.-л. исчисления (формальной системы) П. в., формулируемые на метаязыке данного исчисления, представляют собой содержательно понимаемые правила перехода от одних формальных выражений предметного языка к другим. Если посылки П. в. являются теоремами, то таковым будет и заключение; если же о доказуемости посылок ничего не известно, то говорят просто о выводе из посылок (гипотез). На совокупность П. в. данной формальной системы a priori не накладывается никаких ограничений, кроме их совместимости (или непротиворечивости), и в этом смысле они ничем принципиально не отличаются от др. постулатов – аксиом в собств. смысле слова (являющихся формулами предметного языка, а не высказываниями о таковых). Аналогичным же образом для П. в. ставятся проблемы независимости и полноты. В то же время для П. в. особенную важность и остроту приобретает вопрос об их с е м а н т и ч е с к о м "оправдании" (обосновании), поскольку П. в. конкретных исчислений в той или иной мере претендуют на "адекватное" отображение "норм правильного мышления". "Допустимость" ("правильность") П. в. означает не что иное, как соответствие их нек-рым семантич. требованиям (см. Семантика в логике). Примером такого рода требований может служить соответствие одному из след. трех определений:

(1) из А1 ..., Аn л о г и ч е с к и с л е д у е т В тогда и только тогда, когда для всякой непустой области для любого набора значений свободных переменных, при к-ром формулы А1 ..., Аn принимают значение "истина", В также принимает значение "истина".

(2) Из А1, ..., Аn слабо следует В тогда и только тогда, когда для всякой непустой области, если А1, ..., Аn в ней общезначимы (т.е. принимают значение "истина" для всех наборов значений свободных переменных из этой области), В также общезначима в этой области.

(3) Формула В н а с л е д у е т св-во универсальной общезначимости системы формул А1, ..., Аn тогда и только тогда, когда из универсальной общезначимости А1, ..., Аn следует универсальная общезначимость (общезначимость во всех непустых областях) формулы В.

Соответственно введенным трем семантич. отношениям между формулами можно ввести понятие допустимого П. в. первого, второго и третьего типов: есть допустимое П. в. первого типа, если из А1, ..., Аn логически следует В; аналогично для второго и третьего типов. Так, 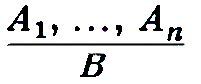есть допустимое П. в. первого (а тем самым второго и третьего) типа, но 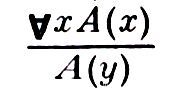не есть допустимое П. в. первого, а только второго (и тем самым третьего) типа.

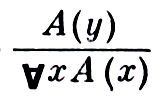Были построены исчисления, в рамках к-рых удалось полностью формализовать св-во универсальной общезначимости формул логики предикатов первого порядка – таковым является исчисление предикатов первого порядка. Более того, П. в. узкого исчисления предикатов, сформулированные для формализации св-ва универсальной общезначимости, формализуют и отношение слабого следования (т.е. они оказываются допустимыми П. в. не только третьего, но и второго типа: из А1, ..., Аn слабо следует В тогда и только тогда, когда существует формальный вывод В из А1, ..., Аn).

Если не налагать на определения П. в. никаких ограничений, то неизвестно, можно ли формализовать на их основе отношение логич. следования. Во всяком случае т.н. правила Бернайса и 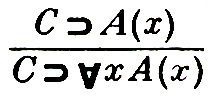или их эквиваленты не воспроизводят полностью отношения логич. следования. Но полная формализация логич. следования может быть осуществлена путем наложения на применение П. в., не являющихся П. в. первого типа, т.е. правил Бернайса, нек-рых ограничений (см. Предикатов исчисление).

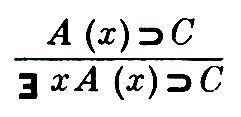См. такжест.: Вывод, Исчисление, Натуральное исчисление.

Лит.: Клини С. К., Введение в метаматематику, пер. с англ., М., 1957, § 19, 23, 77; Черч Α., Введение в математическую логику, пер. с англ., т. 1, М., 1960, § 07; Смирнова Е. Д., Формализованные языки и логическая форма, в сб.: Логическая структура научного знания, М., 1965; Слупецкий Е., Борковский Л., Элементы математической логики и теория множеств, пер. с польск., М., 1965; Lorenzen P., Einführung in die operative Logik und Mathematik, B. – [u. a.], 1955.