Akademik

- система обыкновенных дифференциальных уравнений для 2га неизвестных ("обобщенные импульсы") и ("обобщенные координаты"), имеющая вид:

где Н- нек-рая функция от наз. Гамильтона функцией, или гамильтонианом, системы (1).

Г. с. наз. также каноническими, а в автономном случае (когда Нне зависит явно от t).иногда и консервативными системами, поскольку в этом случае функция Н(имеющая во многих примерах физич. смысл энергии) является первым интегралом (т. е. энергия сохраняется при движении). В механике Г. с. описывают движение при голономных связях и силах, имеющих потенциал (см. Гамильтона уравнения). Многие задачи теоретич. физики также приводят к Г. с. или к таким уравнениям с частными производными, к-рые имеют близкие свойства и могут рассматриваться как бесконечномерные аналоги Г. с. Уравнениям квантовой механики можно придать вид Г. с., в к-рых, однако, p_i(t) и q_i(t)являются не числовыми функциями времени, а (зависящими от t).самосопряженными линейными операторами, удовлетворяющими определенным перестановочным соотношениям. Г. с. (в обычном смысле слова) играют важную роль при исследованиях нек-рых асимптотич. задач для уравнений с частными производными (коротковолновая асимптотика для волнового уравнения, квазиклассич. асимптотика в квантовой механике).

Тесно связаны с Г. с. различные вариационные принципы. Принцип Гельмгольца (см., напр., [3]) непосредственно приводит к Г. с., однако он употребляется редко. Наибольшее значение имеет Гамильтона- Остроградского принцип (стационарного действия принцип), к-рый непосредственно приводит к Лагранжа уравнениям;при выполнении нек-рых дополнительных условий типа невырожденности от последних можно перейти к Г. с. с помощью Лежандра преобразования (см. Гамильтона функция, Гамильтона уравнения), если в вариационный принцип входят производные только первого порядка. Несколько сложнее осуществляется предложенный М. В. Остроградсиим переход к Г. с. в том случае, когда вариационный принцип содержит производные порядка выше первого (см., папр., [4]. § 110). Если Hнезависит явно от q_i, то p_i=const - первый интеграл. В этом случае координату q_i наз. циклической (в нек-рых случаях она имеет физич. или геометрич. смысл угловой переменной), или игнорируемой. Такую координату q_i и соответствующий ей импульс p_i можно исключить и тем самым перейти к Г. с. с меньшим числом неизвестных. Более общо, при наличии kнезависимых первых интегралов в инволюции возможно понижение порядка Г. с. на 2k (по крайней мере в нек-рой области изменения переменных и с заменой времени), и при этом снова получается Г. с. Если все координаты циклические, то Г. с. наз. (вполне) интегрируемой; нахождение ее решений и качественное исследование их свойств уже не требует решения дифференциальных уравнений.

Первые интегралы Г. с. часто получаются из теоремы Нётер: если функция Лагранжа (или лагранжиан) инвариантна относительно некоторой непрерывной группы преобразований, то соответствующая Г. с. имеет первые интегралы определенного вида (см., напр., [2]). Другое общее соображение, позволяющее иногда проинтегрировать Г. с., состоит в переходе к вспомогательному уравнению с частными производными - так наз. уравнению Гамильтона - Якоби (см. Гамильтона - Якоби теория). Посредством разделения переменных в подходящих координатах иногда удается найти полный интеграл последнего, тогда теорема Якоби позволяет сравнительно легко проинтегрировать Г. с. [Связь между Г. с. и уравнением Гамильтона - Якоби является двусторонней: решение последнего сводится к интегрированию соответствующей Г. с. Исторически эта связь вместе с аналогией между механикой и геометрич. оптикой (см. [1], с. 548, [2] или [3], с. 421, 451) способствовала открытию Г. с. (принцип Гюйгенса в оптике сразу приводит к эйконала уравнению - уравнению типа уравнения Гамильтона - Якоби).]

Для Г. с., близких к интегрируемым, разработаны специфич. методы приближенного интегрирования и качественного исследования свойств решений. Родственные методы служат также для исследования поведения траекторий Г. с. в окрестности положений равновесия, периодич. или квазипериодич. решений. Могут использоваться и методы, не связанные специально с Г. с., однако и тогда специфика Г. с. может позволить упростить вычисления или, наоборот, усложнить задачу (поскольку с точки зрения общего метода Г. с. могут оказаться "исключительными" - так, напр., обстоит дело с устойчивостью). См. Адиабатический инвариант, Малого параметра метод, Малые знаменатели, Осреднение.

Пусть - решение Г. с. (1), проходящее при t=0через точку . Г. с. однозначно характеризуется тем, что (локальные) диффеоморфизмы переводят внешнюю дифференциальную форму

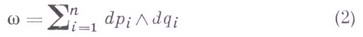
(так наз. интегральный инвариант Пуанкаре) снова в со; этот факт в других терминах отмечался еще М. В. Остроградским и Г. Гельмгольцем (Н. Helmholtz); последний говорил о "свойстве взаимности" (см. [3]). Диффеоморфизмы, сохраняющие w, наз. каноническими преобразования-м и (или каноническими заменами переменных); они не только естественно возникают из Г. с., но и переводят любую Г. с. снова в Г. с. (Последним свойством обладают и обобщенные канонич. преобразования, переход к к-рым, впрочем, не является особенно существенным расширением рассматриваемого класса преобразований.) При этом гамильтониан новой системы легко выражается через исходный гамильтониан и производящую функцию Sканонич. преобразования (которое удобно задавать именно с помощью S). Таким образом, имея дело с Г. с. и производя канонич. замену переменных, можно производить вычисления всего с двумя функциями Ни S(тогда как в общем случае замены переменных в системе дифференциальных уравнений пришлось бы рассматривать гораздо больше функций); в этом состоит так наз. канонический формализм, существенно упрощающий вычисления в пределах своей применимости. Он широко используется в небесной механике и теоретич. физике.

Определение Г. с. в терминах интегрального инварианта приводит к естественному обобщению, когда вместо формы (2) в речь идет о заданной на нек-ром многообразии Мчетной размерности 2п внешней дифференциальной форме 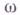2-го порядка, причем замкнута (внешний дифференциал 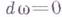) и всюду 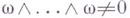(тогда говорят, что на Мзадана симплектическая структура.) Еще более общей является трактовка Г. с. не как динамической системы, а как конгруэнции, когда траектории рассматривают просто как семейство линий с определенными свойствами и не обращают внимания на скорость движения по ним. 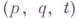(Систему (1) можно включить в эту схему, рассматривая графики решений в пространстве ; при этом вместо (2) большую роль играет интегральный инвариант Пуанкаре - Картава ) Собственно, когда с помощью первых интегралов понижается порядок Г. с. (1), то получается Г. с. именно в этом обобщенном смысле (см. [2]).

О свойствах Г. с., не являющихся интегрируемыми или близкими к таковым, известно мало (не считая названных выше вопросов о локальном поведении траекторий). Сохранение w влечет сохранение элемента объема ш" (теорема Лиувилля; обратное неверно, исключая малые размерности).

Поэтому Г. с. принадлежат к числу систем с инвариантной мерой, изучаемых в эргодической теории.

Лит.:[1] Парс Л.-А., Аналитическая динамика, пер. с англ., М., 1971; [2] Арнольд В. И., Математические методы классической механики, М., 1974; [3]Леви-Чивита Т., Амальди У., Курс теоретической механики, пер. с итал., М., 1951, т. 2, ч. 2; [4] Уиттекер Е. Т., Аналитическая динамика, М.-Л., 1937. Д. В. Аносов.