алгебра Грассма-н а, векторного пространства Vнад полем k - ассоциативная алгебра над k, операция в к-рой обозначается знаком  , порождающими элементами к-рой являются
, порождающими элементами к-рой являются  где
где  - базис пространства V, а определяющие соотношения имеют вид
- базис пространства V, а определяющие соотношения имеют вид
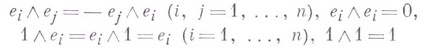
В. а. не зависит от выбора базиса и обозначается  Подпространство
Подпространство 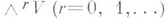 в
в 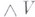 , порожденное элементами вида
, порожденное элементами вида  наз. r-й внешней степенью пространства V. Имеют место равенства:
наз. r-й внешней степенью пространства V. Имеют место равенства: Кроме того,
Кроме того,
Элементы пространства  наз.
наз. 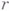 -векторами; их можно понимать также как кососимметрические г раз контраварнантные тензоры в V(см. Внешнее произведение).
-векторами; их можно понимать также как кососимметрические г раз контраварнантные тензоры в V(см. Внешнее произведение).
r-векторы тесно связаны с r-мерными подпространствами в V: линейно независимые системы векторов  н
н 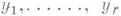 из V порождают одно и то же подпространство тогда и только тогда, когда r-векторы
из V порождают одно и то же подпространство тогда и только тогда, когда r-векторы  и
и  пропорциональны. Этот факт был одним из отправных пунктов в исследованиях Г. Грассмана [1], к-рый ввел В. а. как алгебраич. аппарат для описания порождения многомерных подпространств одномерными. С помощью В. а. легко строится теория определителей. В. а. может быть определена и для более общих объектов, а именно, для унитарных модулей Мнад коммутативным кольцом А с единицей (см. [4]). r-я внешняя степень
пропорциональны. Этот факт был одним из отправных пунктов в исследованиях Г. Грассмана [1], к-рый ввел В. а. как алгебраич. аппарат для описания порождения многомерных подпространств одномерными. С помощью В. а. легко строится теория определителей. В. а. может быть определена и для более общих объектов, а именно, для унитарных модулей Мнад коммутативным кольцом А с единицей (см. [4]). r-я внешняя степень 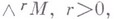 модуля Мопределяется как фактормодуль r-й тензорной степени этого модуля по подмодулю, порожденному элементами вида
модуля Мопределяется как фактормодуль r-й тензорной степени этого модуля по подмодулю, порожденному элементами вида 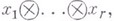 где
где 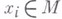 и
и  для нек-рых
для нек-рых 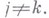 В. а. для Мопределяется как прямая сумма
В. а. для Мопределяется как прямая сумма 
 где
где  с естественно введенным умножением. В случае конечномерного векторного пространства это определение совпадает с первоначальным. В. а. модуля находит применение в теории модулей над кольцом главных идеалов (см. [5]).
с естественно введенным умножением. В случае конечномерного векторного пространства это определение совпадает с первоначальным. В. а. модуля находит применение в теории модулей над кольцом главных идеалов (см. [5]).
Грассмaновыми (или плюккеровыми) координатами r-мерного подпространства Lв гс-мерном пространстве Vнад kназ. координаты r-вектора в V, соответствующего L, к-рый определен с точностью до пропорциональности. С помощью грасс-мановых координат множество всех r-мерных подпространств в Vестественным образом вкладывается в проективное пространство размерности 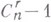 и оказывается там алгебраич. многообразием (наз. Грассмана многообразием).
и оказывается там алгебраич. многообразием (наз. Грассмана многообразием).
Этот метод позволяет построить целый ряд важных примеров проективных алгебраич. многообразий [6].
В форме исчисления внешних дифференциальных форм В. а. используется в качестве одного из основных формализмов в дифференциальной геометрии (см. [8], [7]). В терминах В. а. формулируются многие важные результаты алгебраич. топологии.
Например, если G - конечномерное H-пространство (например, группа Ли), то алгебра 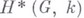 когомологий пространства Gс коэффициентами в поле kхарактеристики нуль является В. а. с образующими нечетных степеней. Если G - односвязная компактная группа Ли, то В. а. (над кольцом целых чисел) является также кольцо
когомологий пространства Gс коэффициентами в поле kхарактеристики нуль является В. а. с образующими нечетных степеней. Если G - односвязная компактная группа Ли, то В. а. (над кольцом целых чисел) является также кольцо 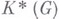 , изучаемое в К-те-ории.
, изучаемое в К-те-ории.
Лит.:[1] Grassmann H., Gesammelte mathematische imd physikalische Werke, Bd 1, Tl. 1-2, Lpz., 1894-96; [2] Мальцев А. И., Основы линейной алгебры, 2 изд., М., 1956; [3] Калужнин Л. А., Введение в общую алгебру, М., 1973; [4] Бур баки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [5] его же, Алгебра. Модули, кольца, формы, пер. с франц., М., 1968; [6] Ходж В., Пидо Д., Методы алгебраической геометрии, пер. с англ., т. 1-3, М., 1954; [7] Фиников С. П., Метод внешних форм Картана в дифференциальной геометрии, М.-Л., 1948; К] Стернберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970. А. Л. Онищик.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.