Akademik

- топологическая группа, компактная как топологич. пространство. Напр., всякая конечная группа (в дискретной топологии) является К. г. Алгебраическая группа, хотя она и является компактным топологич. пространством (относительно топологии Зариского), не будет топологич. группой относительно этой топологии и потому не будет К. г.

Два важнейших типа К. г. представляют следующие группы. 1) Локально связные компактные группы. Примерами таких К. г. являются группа U(n, С) всех унитарных комплексных матриц порядка п, группа О( п, R )всех ортогональных вещественных матриц порядка п(с топологией, индуцированной топологией полей С и R соответственно, определенной обычным абсолютным значением) и, более общо, любая компактная вещественная группа Ли. 2) Вполне несвязные компактные группы. Такова группа GL(n, Z_p )невырожденных матриц порядка пс коэффициентами в кольце Z _р целых р- адических чисел (с тополргией, индуцированной топологией кольца Z_p, определенной р-адическим нормированием) (см. Вполне несвязное пространство).

Любая вполне несвязная К. г. является проконечной группой, и обратно, всякая проконечная группа будет вполне несвязной К. г. Вполне несвязные хаусдорфовы К. г. могут быть охарактеризованы как К. г. нулевой топологич. размерности. Если же G локально связна и конечномерна, то G - вещественная группа Ли [1]. Структура К. г. общего вида до нек-рой степени определена структурой этих двух типов К. г. А именно: в произвольной конечномерной К. г. Gимеется такой нульмерный нормальный делитель N(лежащий в центре группы G), что G/N- вещественная группа Ли и, более того, нек-рая окрестность единицы в Gявляется прямым произведением группы Nи вещественной Ли локальной группы. Всякая связная конечномерная К. г. имеет вид где Р- односвязная компактная полупростая вещественная группа Ли, С-связная конечномерная коммутативная К. г., a Z - конечный центральный нормальный делитель, у к-рого лишь единица лежит в С. Изучение строения связных компактных вещественных групп Ли доведено до их полной классификации (см. Ли компактная группа);строение коммутативных К. г. выясняется в теории двойственности Понтрягина. Любая К. г. (не обязательно конечномерная) является проективным пределом компактных вещественных групп Ли [2]. Топологич. строение указанных двух типов К. г. следующее: всякая локально связная конечномерная К. г. является топологич. многообразием, а всякая бесконечная нульмерная К. г. со счетной базой гомеоморфна канторову совершенному множеству.

Изучение строения К. г. основано на том, что всякая К. г. Gобладает достаточной системой конечномерных линейных представлений, т. е. для любого элемента существует такое непрерывное конечномерное линейное представление р, для к-рого Этот факт является одним из ва?кных результатов далеко развитой общей теории линейных представлений К. г. Эта теория существенно использует то, что каждая К. г. обладает двусторонне инвариантной мерой m(g), к-рая позволяет определить на Gинвариантное интегрирование. Важнейшие факты этой теории состоят в следующем. Всякое непрерывное представление К. г. Gв предгильбертовом пространстве эквивалентно унитарному представлению. Пусть L²(G)- гильбертово пространство интегрируемых с квадратом по инвариантной мере m(g) комплекснозначных функций на G. Действие группы Gна функции левыми и правыми сдвигами определяет на L²(G)структуры левого и правого G-модулей. Соответствующие представления наз. соответственно левым и правым регулярным представлением группы G; они унитарны и унитарно эквивалентны. Пусть - семейство всевозможных попарно неэквивалентных конечномерных неприводимых унитарных представлений К. г. Gи i, j=1, 2, ..., n_a=dim R^a -набор матричных элементов представления R^a в некотором ортонормированном базисе. Тогда функции лежат в L²(G)и образуют там полную ортонормированную систему, причем норма функции равна Любая непрерывная на Gкомплекснозначная функция может быть с любой точностью равномерно аппроксимирована конечными линейными комбинациями функций 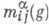(теорема Петера - Вейля). Характеры неприводимых унитарных конечномерных представлений попарно ортогональны и имеют норму 1. Непрерывные конечномерные унитарные представления эквивалентны тогда и только тогда, когда их характеры равны. Непрерывное конечномерное унитарное представление неприводимо тогда и только тогда, когда норма его характера (который лежит в L²(G))равна 1. Всякое неприводимое непрерывное унитарное представление группы G в гильбертовом пространстве конечномерно Всякое непрерывное унитарное представление группы, в гильбертовом пространстве является ортогональной прямой суммой унитарных представлений, кратных конечномерным неприводимым представлениям. В частности, кратность вхождения представления R^a в правое регулярное представление равна /i_a=dim R^a; при этом сумма всех G-подмодулей в G-модуле L²(G), изоморфных R^a, является в точности линейной оболочкою всех функций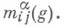

Лит.:[1] Понтрягин Л. С, Непрерывные группы 3 изд., М., 1973; [2] Вейль А., Интегрирование в тополо гических группах и его применения, М., 1950; [3] Наймарн М. А., Теория представлений групп, М., 1976; [4] Желобенко Д. П., Компактные группы Ли и их представления, М. 1970. В. Л. Попов