Akademik

- мономорфизм кольца в некоторое другое кольцо; кольцо Rвкладывается в кольцо L, если Rизоморфно подкольцу кольца L. Наиболее подробно изучались условия вложения ассоциативного кольца в (ассоциативное) тело и произвольного кольца в кольцо с делением. Начало этим исследованиям положила работа А. И. Мальцева [1], в которой был построен пример ассоциативного кольца без делителей нуля, не вложимого в тело. Долгое время оставалась открытой следующая проблема Мальцева: будет ли вложимо в тело каждое ассоциативное кольцо без делителей нуля, полугруппа ненулевых элементов к-рого вложима в группу? Эта проблема была решена отрицательно в 1966 (см. [2], с. 354). Квадратная матрица Апорядка над ассоциативным кольцом R наз. неполной, если она предета-вима в виде , где 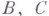- матрицы порядков 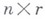и соответственно и r<n. Пусть

- квадратные матрицы порядка над R, у к-рых совпадают все столбцы, кроме, возможно, первого. Тогда матрица 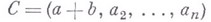наз. детерминантной суммой матриц А и Вотносительно первого столбца. Аналогично определяется детерминантная сумма квадратных матриц одинаковых порядков относительно произвольного столбца (строки). Ассоциативное кольцо R с 1 вложимо в тело тогда и только тогда, когда оно не имеет делителей нуля и никакая скалярная матрица аЕ с ненулевым элементом апо диагонали не может быть представлена в виде детерминантной суммы конечного числа неполных матриц ([2], с. 349). Класс ассоциативных колец, вложимых в тела, не является конечно аксиоматизируемым (т. е. его нельзя задать конечным числом аксиом) [3]. Известен ряд достаточных условий вложения ассоциативного кольца в тело. Наиболее важными из них являются следующие. Пусть R - ассоциативное кольцо без делителей нуля, полугруппа ненулевых элементов к-рого удовлетворяет условию Оре (см. Вложение полугруппы). Тогда кольцо Rвложимо в тело ([4], с. 293). Групповая алгебра упорядоченной группы вложима в тело (теорема Мальцева- Неймана, см. [4], с. 294). Произвольная область свободных правых (левых) идеалов (см. Ассоциативные кольца и алгебры).вложима в тело ([2], с. 351).

Кольцо Rвложимо в кольцо с делением тогда и только тогда, когда оно не содержит делителей нуля. Пусть R, L - кольца, - символ, 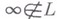. Отображение наз. Т- гомоморфизмом; если: 1) множество есть кольцо и отображение на атом множестве есть кольцевой гомоморфизм; 2) из следует 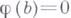; 3) из 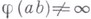, 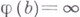следует . T-гомоморфизм поля есть не что иное, как специализация (или точка) поля. Кольцо с делением L наз. свободным T-расширением кольца R, если: Lсодержит Rи порождается (как кольцо с делением) кольцом R, а любой T-гомомор-физм кольца Rв некоторое кольцо с делением Sможно продолжить до T-гомоморфизма Lв S. Каждое кольцо без делителей нуля обладает свободным T-расширением ([4], с. 301).

Лит.:[1] Мальцев А. И., "Math. Ann.", 1937, Bd 113, S. 686-691; [2] Кон П. М., Свободные кольца и их связи, пер. с англ., М., 1975; [3] Соhn Р. М., "Bull. Lond. Math. Soc.", 1974, v. 6, p. 147-148; [4] Кон П, М., Универсальная алгебра, пер. с англ., М., 1968. Л. А. Вокуть.