Akademik

-одна из классических ортонормированных систем непрерывных функций. Ф. с. (см. [1] или [2]) получается применением процесса ортогонализации Шмидта на отрезке [0, 1] к Фабера - Шаудера системе, построенной с помощью множества всех двоично рациональных точек отрезка [0,1]; в этом случае система Фанера - Шаудера с точностью до постоянных множителей совпадает с системой , где -Хаара система.
Ф. с. является исторически первым примером базиса в пространстве непрерывных функций, обладающего свойством ортогональности. Эта система также является базисом во всех пространствах L_p[0, 1], (см. [3]). Если непрерывная на отрезке [0,1] функция f(t) имеет модуль непрерывности 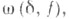a S_n(t, f) - частная сумма порядка пряда Фурье функции f(t) по системе Франклина, то

При этом коэффициенты Фурье - Франклина а _п(f) функции f(t) удовлетворяют неравенствам

a условия:

при являются равносильными. Если непрерывная функция f(t) такова, что

то ряд

сходится на отрезке [0, 1] равномерно, а если

то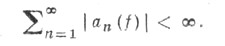

Все эти свойства Ф. с. доказываются с помощью неравенства

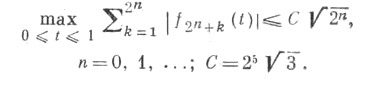
Ф. с. является безусловным базисом во всех пространствах и, более того, во всех рефлексивных пространствах Орлича (см. [5]). Если функция f(t)принадлежит пространству L_p[0, 1], 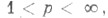то имеют место неравенства

где обозначает норму в пространстве L_p[0, 1], а постоянные А _р> 0 и В _р>0 зависят лишь от р.
Ф. с. нашла важные приложения в различных вопросах анализа. В частности, с помощью этой системы были построены базисы в пространствах С ¹ (I²) (см. [4]) и A(D)(см. [5]). Здесь С ¹(I²) - пространство всех непрерывно дифференцируемых на квадрате функций f(x, f )с нормой

a A(D) - пространство всех функции f(z) с нормой

аналитических в открытом круге D = {z:|z]|<1} комплексной плоскости и непрерывных в замкнутом круге Вопросы о существовании базисов в пространствах С ¹(I²) и A(D)были поставлены С. Банахом [6].

Лит.:[l] Franklin P., лMath. Ann.