- варианты описания автоматов, их функционирования или поведения. А. с. з. зависят от подхода к определению понятия автомата. При макроподходе (см. Автомат конечный).описывается внешнее поведение автомата; при микроподходе задание должно содержать описание элементов, из к-рых строится автомат, и схемы их соединения. Ниже приводятся способы задания конечных автоматов.
Макроподход. В этом случае задать конечный автомат  при условии, что заданы алфавиты значит
при условии, что заданы алфавиты значит 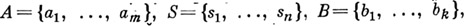 описать функции
описать функции  или описать поведение этого автомата (см. Автомата поведение). Для задания функций
или описать поведение этого автомата (см. Автомата поведение). Для задания функций 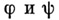 обычно используют таблицу переходов, диаграмму переходов или матрицу переходов. Таблица переходов Тавтомата
обычно используют таблицу переходов, диаграмму переходов или матрицу переходов. Таблица переходов Тавтомата  состоит из двух подтаблиц
состоит из двух подтаблиц 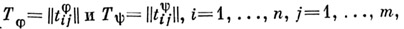
 , Функции
, Функции 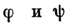 определяются как
определяются как 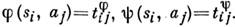 Если все столбцы
Если все столбцы  совпадают, то таблица Тзадает автомат Мура. Напр., пусть
совпадают, то таблица Тзадает автомат Мура. Напр., пусть  тогда таблица Т(рис. 1) задает функции
тогда таблица Т(рис. 1) задает функции  нек-рого автомата
нек-рого автомата  (на рис. 2 показаны подтаблицы
(на рис. 2 показаны подтаблицы  таблицы Т).
таблицы Т).
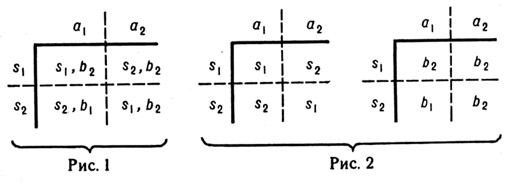
Диаграмма автомата (диаграмма переходов автомата) - это ориентированный граф G, вершинам к-рого взаимно однозначно соответствуют элементы 5, а ребрам приписаны нек-рые множества пар вида  Из каждой вершины G исходит по крайней мере одно ребро; при этом множество
Из каждой вершины G исходит по крайней мере одно ребро; при этом множество  всех пар, приписанных ребрам, исходящим из одной вершины, имеет вид
всех пар, приписанных ребрам, исходящим из одной вершины, имеет вид 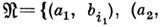
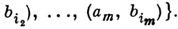 Функции j и y) определяются следующим образом:
Функции j и y) определяются следующим образом: если ребру, исходящему из вершины si , приписана пара ( а i , b р).и это ребро ведет в вершину sr . Нек-рые свойства автоматов удобно формулировать на
если ребру, исходящему из вершины si , приписана пара ( а i , b р).и это ребро ведет в вершину sr . Нек-рые свойства автоматов удобно формулировать на
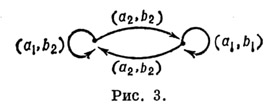
языке диаграмм (связность автомата, достижимость состояний и т. п.). На рис. 3 представлена диаграмма переходов автомата 
Матрица переходов используется для описания функционирования переходной системы  (см. Автомат конечный). Она представляет собой
(см. Автомат конечный). Она представляет собой
 элементами к-рой являются подмножества алфавита А(может быть, пустые) такие,
элементами к-рой являются подмножества алфавита А(может быть, пустые) такие,
что  тогда и только тогда, когда
тогда и только тогда, когда  и, следовательно, для всякого
и, следовательно, для всякого 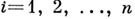 имеет место
имеет место  Чтобы распространить функцию
Чтобы распространить функцию  на множество
на множество  (.
(. - множество всех слов в алфавите А, включая пустое слово), рассматривают последовательность степеней матрицы Р. Умножение матрицы Рна себя производится по обычному алгоритму с использованием вместо операций умножения и сложения операций произведения (к о н-катенации) и объединения множеств слов. Если
- множество всех слов в алфавите А, включая пустое слово), рассматривают последовательность степеней матрицы Р. Умножение матрицы Рна себя производится по обычному алгоритму с использованием вместо операций умножения и сложения операций произведения (к о н-катенации) и объединения множеств слов. Если 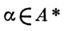 - слово длины
- слово длины  - элемент матрицы
- элемент матрицы  Так, матрица переходов Рпереходной системы
Так, матрица переходов Рпереходной системы 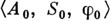 и матрица
и матрица 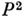 имеют, соответственно, вид:
имеют, соответственно, вид:

С указанными А. с. з. связан ряд алгоритмов минимизации (приведения) и синтеза автоматов.

Для задания поведения инициального (не обязательно конечного) автомата  (преобразователя) необходимо описать функцию
(преобразователя) необходимо описать функцию  отображающую
отображающую 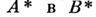 (или
(или 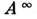 в
в 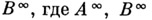 - множества всех сверхслов в алфавитах Аи В, соответственно). Эта функция может быть задана информационным деревом. Из каждой вершины информационного дерева исходит
- множества всех сверхслов в алфавитах Аи В, соответственно). Эта функция может быть задана информационным деревом. Из каждой вершины информационного дерева исходит 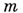 ребер, взаимно однозначно соответствующих буквам алфавита
ребер, взаимно однозначно соответствующих буквам алфавита  . Каждой вершине приписано состояние автомата
. Каждой вершине приписано состояние автомата  а каждому ребру - буква алфавита Вследующим образом. Корню приписано состояние
а каждому ребру - буква алфавита Вследующим образом. Корню приписано состояние 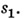 Если нек-рой вершине приписано состояние
Если нек-рой вершине приписано состояние  то ребру, соответствующему букве
то ребру, соответствующему букве  приписана буква
приписана буква  и вершине, в к-рую ведет это ребро, приписано состояние
и вершине, в к-рую ведет это ребро, приписано состояние 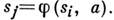 Каждому слову
Каждому слову 
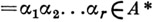 соответствует единственная последовательность
соответствует единственная последовательность  ребер этого дерева такая, что
ребер этого дерева такая, что  исходит из корня и
исходит из корня и  исходит из вершины, в к-рую ведет
исходит из вершины, в к-рую ведет  Слово
Слово 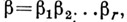 где
где  - буква из В, приписанная ребру
- буква из В, приписанная ребру 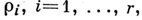 совпадает со значением
совпадает со значением  Если функция f реализуется конечным автоматом, то соответствующее информационное дерево может быть задано эффективно своим конечным поддеревом. На рис. 4 изображено поддерево информационного дерева, задающее поведение инициального автомата
Если функция f реализуется конечным автоматом, то соответствующее информационное дерево может быть задано эффективно своим конечным поддеревом. На рис. 4 изображено поддерево информационного дерева, задающее поведение инициального автомата  (левые ребра, исходящие из вершин, соответствуют символу
(левые ребра, исходящие из вершин, соответствуют символу 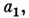 правые - символу
правые - символу 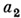 ).
).
Описание поведения конечного автомата (акцептора) в терминах представимого события (сверхсобытия) может быть сделано с помощью регулярного выражения (см. Регулярное событие). Такие события могут быть также заданы как множества слов, порождаемых (выводимых) в нек-рой формальной системе (полу-Туэ грамматике и т. п.). Система полу-Туэ в этом случае задается четверкой 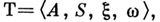 где
где  - конечные алфавиты,
- конечные алфавиты,  - аксиом схема вида
- аксиом схема вида 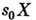 и
и  - множество схем правил вывода вида
- множество схем правил вывода вида 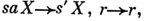 где
где 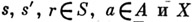 - переменная, принимающая значения из
- переменная, принимающая значения из  . При этом, если
. При этом, если  и
и  принадлежат
принадлежат 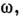 то
то 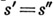 . Слово
. Слово  выводимо в системе
выводимо в системе  если существует последовательность слов
если существует последовательность слов 
 такая, что
такая, что  получается из
получается из 
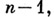 применением нек-рого правила из
применением нек-рого правила из  не содержит правила
не содержит правила  Аналогичный вид имеет грамматика, порождающая регулярное событие. Она задается четверкой
Аналогичный вид имеет грамматика, порождающая регулярное событие. Она задается четверкой 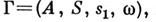 где
где  из
из 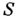 - аксиома,
- аксиома,  - множество правил вида
- множество правил вида  либо
либо 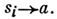
Слово 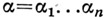 выводимо в Г, если в w имеются правила
выводимо в Г, если в w имеются правила  Известны алгоритмы, позволяющие получать матрицу переходов автомата по формальным системам описанного типа. Так, событие, представимое в акцепторе
Известны алгоритмы, позволяющие получать матрицу переходов автомата по формальным системам описанного типа. Так, событие, представимое в акцепторе  состоянием
состоянием 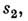 может быть, напр., задано как множество слов, выводимых в системе полу-Туэ, к-рая имеет вид:
может быть, напр., задано как множество слов, выводимых в системе полу-Туэ, к-рая имеет вид:

Существует ряд других А. с. з. Напр., переходная система  не обязательно конечная, может быть задана как алгебра
не обязательно конечная, может быть задана как алгебра  где
где  есть множество унарных операций на
есть множество унарных операций на  таких, что
таких, что 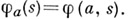 Так, переходную систему
Так, переходную систему  можно рассматривать как алгебру
можно рассматривать как алгебру 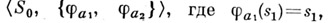
 Можно также рассматривать алгебру
Можно также рассматривать алгебру 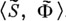 , где
, где 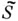 - множество слов вида
- множество слов вида  - множество унарных операций на
- множество унарных операций на  таких, что
таких, что  Алгебра
Алгебра  задается системой образующих Sи множеством определяющих соотношений
задается системой образующих Sи множеством определяющих соотношений 
Такая алгебра задает автомат воооще говоря, частичный) 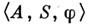 такой, что если
такой, что если  - соотношение из
- соотношение из  Напр., переходную систему
Напр., переходную систему  можно задать системой образующих
можно задать системой образующих  и множеством определяющих соотношений
и множеством определяющих соотношений 
 При этом предполагается, что
При этом предполагается, что 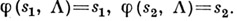
Поведение автомата может быть описано средствами языка логики одноместных предикатов. При этом выбор класса формул, задающих конечные автоматы, осуществляется различными способами. Описание может быть неполным, тогда оно определяет нек-рый класс автоматов, поведение к-рых идентично с точностью до этого описания. Напр., "анкетный" подход связан с заданием класса автоматов с помощью фрагментов информационных деревьев, частичного определения функций j и y и т. п.
Указанные А. с. з. могут быть использованы с соответствующими модификациями при макроподходе к поведению нек-рых обобщений конечных автоматов (недетерминированных, бесконечных и т. п., см. Автомат), Так, элементами таблицы  конечного недетерминированного автомата могут быть произвольные подмножества множества S. Поведение конечного недетерминированного акцептора описывается регулярным выражением, как и в детерминированном случае. Другими обобщениями конечных автоматов являются конечные автоматы вероятностные, автоматы над термами, мозаичные структуры и т. п.
конечного недетерминированного автомата могут быть произвольные подмножества множества S. Поведение конечного недетерминированного акцептора описывается регулярным выражением, как и в детерминированном случае. Другими обобщениями конечных автоматов являются конечные автоматы вероятностные, автоматы над термами, мозаичные структуры и т. п.
Задать вероятностный автомат 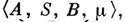 если известны алфавиты
если известны алфавиты 
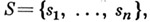 - значит при любых фиксированных iи
- значит при любых фиксированных iи  указать условную вероятностную меру |
указать условную вероятностную меру | на множестве всех пар
на множестве всех пар 
 Для этого обычно рассматривают систему квадратных матриц с неотрицательными элементами
Для этого обычно рассматривают систему квадратных матриц с неотрицательными элементами

такую, что каждая матрица 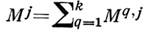 является стохастической. Мера
является стохастической. Мера 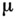 определяется так:
определяется так: 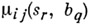
 Вероятностный автомат
Вероятностный автомат  рассматривается совместно с нек-рым начальным распределением вероятностей на множестве
рассматривается совместно с нек-рым начальным распределением вероятностей на множестве 
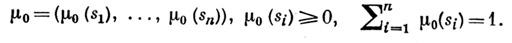
Иногда при задании вероятностных автоматов ограничиваются либо указанием матриц  , либо указанием матриц
, либо указанием матриц  где
где

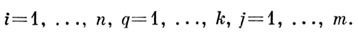 Любая конечная Маркова цепь может рассматриваться как конечный вероятностный автомат, у к-рого матрицы
Любая конечная Маркова цепь может рассматриваться как конечный вероятностный автомат, у к-рого матрицы 
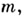 совпадают. Ниже представлены система матриц, задающая нек-рый вероятностный автомат
совпадают. Ниже представлены система матриц, задающая нек-рый вероятностный автомат 
 и матрицы
и матрицы  этого автомата:
этого автомата:

Чтобы задать конечный автомат над термами 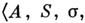
 когда известны алфавиты
когда известны алфавиты 

 необходимо, во-первых, указать отображение а множества Ав конечное множество неотрицательных целых чисел, причем так, чтобы существовал хотя бы один элемент
необходимо, во-первых, указать отображение а множества Ав конечное множество неотрицательных целых чисел, причем так, чтобы существовал хотя бы один элемент  такой, что
такой, что  а во-вторых, для всякого
а во-вторых, для всякого  требуется определить
требуется определить  -местную функцию
-местную функцию  отображающую множество
отображающую множество  Каждому элементу
Каждому элементу 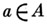 такому, что
такому, что  ставится в соответствие элемент
ставится в соответствие элемент  наз. начальным состоянием автомата. Напр., если
наз. начальным состоянием автомата. Напр., если 
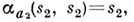 то
то  функции
функции  задают нек-рый автомат над термами
задают нек-рый автомат над термами 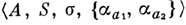 с начальным состоянием
с начальным состоянием 
Чтобы задать мозаичную структуру (бесконечное соединение переходных систем вида 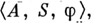 где А
где А  , см. Автомат), необходимо для каждой целочисленной точки n-мерного пространства определить конечное упорядоченное множество целочисленных точек - ее окрестность. При этом входной алфавит Апереходной системы
, см. Автомат), необходимо для каждой целочисленной точки n-мерного пространства определить конечное упорядоченное множество целочисленных точек - ее окрестность. При этом входной алфавит Апереходной системы  помещенной в нек-рую точку, есть декартово произведение множеств состояний переходных систем, помещенных в точки ее окрестности. Напр., пусть
помещенной в нек-рую точку, есть декартово произведение множеств состояний переходных систем, помещенных в точки ее окрестности. Напр., пусть  и для всякой целочисленной точки двумерного пространства
и для всякой целочисленной точки двумерного пространства  ее окрестность
ее окрестность  есть упорядоченное множество
есть упорядоченное множество 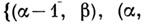
 Чтобы задать однородную двумерную мозаичную структуру, определяют функцию j следующим образом:
Чтобы задать однородную двумерную мозаичную структуру, определяют функцию j следующим образом: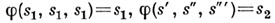 в остальных случаях. Входной алфавит Ав данном случае - декартово произведение
в остальных случаях. Входной алфавит Ав данном случае - декартово произведение 
Микроподход. При микроподходе задать структурный автомат - значит описать элементы, из к-рых он построен, и схему их соединения. Описание может производиться на различных уровнях детализации. Часто ограничиваются рассмотрением так наз. канонической схемы построения автоматов; при этом элементы делят на две группы - функциональные элементы (автоматы с одним состоянием) и элементы памяти. Канонич. схема (рис. 5) состоит из двух функциональных блоков f и gс присоединенными к ним элементами памяти, в качестве к-рых используются автоматы Мура: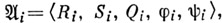
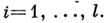 Блоки
Блоки  построены из функциональных элементов. При данном способе задания структуру этих блоков не описывают, а задают (напр., таблично) реализуемые ими вектор-функции:
построены из функциональных элементов. При данном способе задания структуру этих блоков не описывают, а задают (напр., таблично) реализуемые ими вектор-функции:

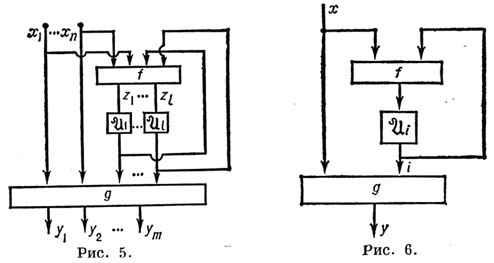
где 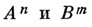 -, соответственно, входной и выходной алфавиты канонич. схемы. Эта схема задает структурный автомат
-, соответственно, входной и выходной алфавиты канонич. схемы. Эта схема задает структурный автомат  , где
, где  а функции
а функции 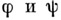 определяются следующим образом:
определяются следующим образом:
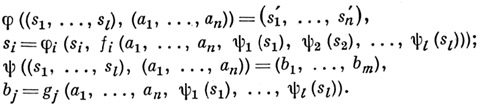
Важным примером структурных автоматов являются логич. сети (см. Автомат конечный). На рис. 6 представлена канонич. схема автомата 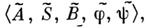 изоморфного автомату
изоморфного автомату  , диаграмма к-рого изображена на рис. 3,
, диаграмма к-рого изображена на рис. 3, 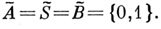 Автомат
Автомат 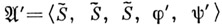 - автомат Мура такой, что
- автомат Мура такой, что 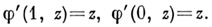
Для описания структурных автоматов часто используются канонические уравнения, т. е. системы вида:

где 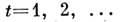 - целочисленный параметр,
- целочисленный параметр,  а функции
а функции  и переменные х r ,
и переменные х r ,  принимают значения из множества А . Этой системе соответствует канонич. схема, в к-рой все элементы памяти совпадают:
принимают значения из множества А . Этой системе соответствует канонич. схема, в к-рой все элементы памяти совпадают:  где
где  Функционирование автомата
Функционирование автомата 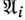 содержательно может быть описано следующим образом. Пусть в момент времени t входу
содержательно может быть описано следующим образом. Пусть в момент времени t входу  приписана буква
приписана буква  тогда эта же буква будет приписана выходу
тогда эта же буква будет приписана выходу 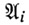 в момент
в момент 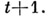 На рис. 6 представлен автомат
На рис. 6 представлен автомат  канонич. уравнения к-рого имеют вид:
канонич. уравнения к-рого имеют вид:

В общем случае описание структурных автоматов связано с заданием набора элементарных автоматов и не-к-рого класса "правильно устроенных" схем (сетей), причем последние обычно определяются индуктивно. Лит.:[1] Автоматы. Сб. статей, пер. с англ., М., 1956; [2] Глушков В. М., Синтез цифровых автоматов, М., 1962.
В. А. Буееич, С. В. Алешин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.