Akademik

СЛУЧАЙНАЯ ВЕЛИЧИНА
одно из основных понятий теории вероятностей. Роль понятий С. в. и ее математического ожидания впервые ясно оценил П. Л. Чебышев (1867, см. [1]) Понимание того факта, что понятие С. в. есть частный случай общего понятия функции, пришло значительно позднее. Полное и свободное от всяких излишних ограничений изложение основ теории вероятностей на основе теории меры дано А. Н. Колмогоровым (1933, см. [2]); оно сделало совершенно очевидным, что С. в. есть ни что иное, как измеримая функция на каком-либо вероятностном пространстве. Это обстоятельство весьма важно учитывать даже при первоначальном изложении теории вероятностей. В учебной литературе эта точка зрения последовательно проведена впервые У. Феллером (см. предисловие к [3], где изложение строится на понятии пространства элементарных событий и подчеркивается, что лишь в этом случае представление о С. в. становится содержательным).
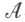Пусть - вероятностное пространство. Однозначную действительную функцию , определенную на , наз. случайной величиной, если при любом действительном хмножество входит в класс . Пусть X - какая-либо С. в. и - класс тех , для к-рых 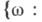это будет -алгебра. Класс всех борелевских подмножеств числовой прямой R1 во всяком случае содержится в 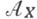. Меру Р Х,определенную на равенством , наз. распределением вероятностей С. в. X. Эта мера однозначно определяется по распределения функции С. в. X, т. е. по функции

Значения вероятностей (т. е. значения меры, служащей продолжением распределения Р Х на -алгебру ) по функции распределения FX однозначно, вообще говоря, не определяются (достаточным для такой однозначности является т. н. условие совершенности меры Р, см. Совершенная мера, а также [4]). Указанное обстоятельство надо постоянно иметь в виду (напр., при доказательстве того, что распределение С. в. однозначно определяется по его характеристической функции).
Если С. в. X принимает конечное или счетное число попарно различных значений х 1, х2, . .., х п,... с вероятностями 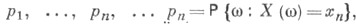то ее распределение вероятностей (называемое в этом случае дискретным) задается формулой

Распределение С. в. X наз. непрерывным, если существует функция 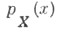(плотностьвероятности) такая, что
для всякого интервала В(или, это то же самое, для любого борелевского множества В). В обычной терминологии математич. анализа это означает абсолютную непрерывность Р Х по отношению к мере Лебега на R1. Ряд общих свойств распределения вероятностей С. в. достаточно полно описывается небольшим количеством числовых характеристик.
При этом медиана и квантили имеют то преимущество, что они определены для любых распределений, хотя наиболее употребительны математическое ожидание и дисперсия DXС. в. X. См. также Вероятностей теория.
Комплексная С. в. Xопределяется парой действительных С. в. Х 1 и Х 2 по формуле
Упорядоченный набор (Х 1, . . ., Xs )С. в. можно рассматривать как случайный вектор со значениями в R s.
Обобщением понятия С. в. на бесконечномерный случай служит понятие случайного элемента.
Следует отметить, что в нек-рых задачах математич. анализа и теории чисел целесообразно рассматривать участвующие в их формулировках функции как С. в., определенные на подходящих вероятностных пространствах (см., напр., [5]).

Лит.:[1] Чебышев II. Л., О средних величинах, в кн.: Полн. собр. соч., т. 2, М.- Л., 1947; [2] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974: [3] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1, М., 1967; [4] Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М.- Л., 1949: [5] Кац М., Статистическая независимость в теории вероятностей, анализе и теории чисел, пер. с англ., М., 1963.
Ю. В. Прохоров.


Математическая энциклопедия. — М.: Советская энциклопедия. . 1977—1985.