Akademik

- функция, представленная как композиция нескольких функций. Если множество значений Y_i функции f_i содержится во множестве определения Х _i+1 функции f_i+1, т. е.

то функция определяемая равенством

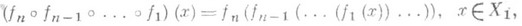
наз. сложной функцией или (п-1)-кратной композицией (суперпозицией) функций f₁, f₂, . . ., f_n. Напр., всякая рациональная функция любого числа переменных является композицией четырех арифметич. действий, т. е. композицией функций х+у, x-у, ху, х/у.

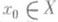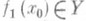С. ф. сохраняет многие свойства функций, композицией к-рых она является. Так, композиция непрерывных функций непрерывна. Это означает, что если функция непрерывна в точке , а функция f₂ : YZ непрерывна в точке , то С. ф. f₂ о/f₁ также непрерывна в точке х ₀ (здесь X, Y и Zявляются, напр., топологии, пространствами). Подобным образом, композиция праз (непрерывно) дифференцируемых функций представляет собой также праз (непрерывно) дифференцируемую функцию, n=1, 2, ... Композиция возрастающих (убывающих) функций есть возрастающая (соответственно убывающая) функция. При композиции функций иногда меняются количественные характеристики свойств функций: композиция функций f₁ и f₂, удовлетворяющих условию Гёльдера нек-рых степеней, есть функция, удовлетворяющая условию Гёльдера степени, равной произведению степеней условий Гёльдера, к-рым удовлетворяют функции f₁ и f₂. Нек-рые характеристики функций не сохраняются при композиции. Так, композиция функций, интегрируемых по Риману или по Лебегу, не является, вообще говоря, функцией, интегрируемой по Риману или, соответственно, по Лебегу; композиция абсолютно непрерывных функций может оказаться не абсолютно непрерывной функцией. Вместе с тем, согласно результатам Н. К. Бари и Д. Е. Меньшова [1], композиция трех абсолютно непрерывных на отрезке функций не приводит к новому классу функций по сравнению с композицией двух абсолютно непрерывных функций. Н. К. Бари [2] доказала, что любая непрерывная на отрезке функция может быть представлена в виде суммы трех композиций абсолютно непрерывных функций, и есть такие непрерывные функции, к-рые но могут быть представлены в виде суммы двух таких композиций. Вместе с тем, всякая непрерывная на отрезке функция является суммой двух композиций функций с ограниченным изменением; однако n-кратные композиции функций с ограниченным изменением для каждого п=1, 2, ... приводят к существенно новым классам функций и существуют однократные композиции функций с ограниченным изменением, не являющиеся непрерывными функциями [3].

Понятие композиции функций представляет собой наиболее широкое понимание термина "представление функции формулой". Задача о представлении функций в виде композиций возникла в связи с отысканием формул для решений алгебраич. уравнений. Всякий корень уравнения степени не выше четвертой может быть представлен формулой, выражающей его через коэффициенты уравнения и представляющей собой композицию четырех арифметич. действий и радикалов. Всякое уравнение степени может быть с помощью подстановки (наз. преобразованием Чирнгаузена) приведено к виду

Таким образом, каждый корень уравнения степени представляет собой функцию п-4 параметров. Задача состоит в выяснении: можно ли эти функции представить в виде композиции алгебраич. функций меньшего числа неременных. Одна из 23 проблем Д. Гильберта (D. Hilbert), поставленных им на Международном конгрессе математиков в Париже в 1900, относилась к этой задаче. Именно, 13-я проблема состояла в следующем (см. [4]): представляется ли корень f уравнения

(*)

через коэффициенты х, у и z этого уравнения посредством композиций каких-либо непрерывных функций двух переменных (следует отметить, что всякая функция конечного числа переменных является композицией разрывных функций двух переменных). Д. Гильбертом была показана невозможность получения всех аналитич. ций трех переменных в виде композиций аналитич. ций двух переменных. Он же для уравнения 9-й степени доказал [5], что решение уравнения 9-й степени можно представить в виде композиции алгебраич. функций четырех переменных (вместо пяти, как это сразу следует из применения преобразования Чирнгаузена). Эти исследования были продолжены многими математиками (см. [6] - [19]).

А. Г. Витушкин в 1954 доказал [10], что если натуральные числа m, п, m₁ и n₁ удовлетворяют неравенству , то можно указать праз дифференцируемую функцию тпеременных, непредставимую в виде композиции n₁ раз дифференцируемых функций от m₁ переменных. В частности, при всяком пможно указать функцию ппеременных наперед заданной гладкости, непредставимую композицией функций меньшего числа переменных той же гладкости. В этом смысле среди гладких функций любого числа переменных существуют функции, существенно зависящие от всех своих аргументов.

В 1956 А. Н. Колмогоров показал [11], что всякая определенная на n-мерном () кубе непрерывная функция является композицией непрерывных функций трех переменных. Затем В. И. Арнольд уменьшил число переменных с трех до двух. Именно, он доказал [12], что любую непрерывную на кубе функцию трех переменных можно представить в виде композиции непрерывных функций двух переменных (и даже, более точно, в виде суммы 9 функций, каждая из к-рых является однократной композицией непрерывных функций двух переменных). Тем самым было показано, что каждая непрерывная на n-мерном () кубе функция представит в виде композиции непрерывных функций двух переменных. Это явилось последним словом по опровержению гипотезы Гильберта о невозможности представления корней уравнения (*) в виде композиций непрерывных функций двух неременных. Работы А. Н. Колмогорова и В. И. Арнольда дали, в частности, положительный ответ на вопрос о представимости корней алгебраич. уравнений любой степени в виде композиции непрерывных функций не более чем двух переменных. Для композиций аналитич. и алгебраич. функций аналогичный вопрос не решен. До сих пор (1983) неизвестно, являются ли корни уравнения (*) композицией аналитич. ций или нет.

Этот цикл работ завершает следующая теорема Колмогорова [13]: любая непрерывная функция гс переменных может быть получена с помощью композиций непрерывных функций одного переменного и единственной функции двух неременных g(x, y) = x+y;именно, он доказал, что любая функция f, непрерывная на n-мерном кубе, может быть представлена в виде

,

где функции h_i и j_ij- непрерывны, а функции j_ij, кроме того, стандартны, т. е. не зависят от выбора функции f.

А. Г. Витушкин показал [14], что для любых конечных наборов непрерывных функций p_k и непрерывно дифференцируемых функций q_k, зависящих от ппеременных, k=1, 2, ..., т, n=1, 2, ..., существуют даже аналитич. ции гс переменных, не представимые композицией вида

где f_k - произвольные непрерывные функции одного переменного.

Лит.: [1]Бари Н. К., Меньшов Д. Е., "Ann. di Mat.", 1927, v. 5, p. 19-54; [2] Бари Н. К., "Math. Ann.", 19,40, Bd 103, S. 185- 248, pt 2, S. 598-653; [3]eе же, "Матем. сб.", 193.Ч, т. 40, с. 326-72; [4] Проблемы Гильберта, М., 1969; [5] Нilbеrt D., "Math. Ann.", 1927, Bd 97, S. 243 - 51; [6] Вieberbасh L., "J. reine u. angew. Math.", 1931, Bd 165, S. 89-92; [7] Чеботарев Н. Г., Собр. соч., т. 1, М.-Л , 1949, с. 255-340; [8]Чеботарев Г. Н., "Уч. заи. Казанск. ун-та",1954, т. 114, кн. 2, с. 189 - 93; [9] Морозов В. В., там же, 1954, т. 114, кн. 2, с. 173-87; [10] Витушкин А. Г., О многомерных вариациях, М., 1955; [11] Колмогоров А. Н., "Докл. АН СССР",

1956. т. 108, №2, с. 179-82; [12] Арнольд В. И., там же,

1957. т. 114, № 4, с. 679-81; [13] Колмогоров А. Н., там же, 1957, т. 114, № 5, с. 953 - 56; [14] Витушкин А. Г., там же, 1964, т. 156, № 6, с. 1258-61; [15] Lоrеntz G. G., Approximation of functions, N. Y.,-[a.o.], 1966; [16] Sprecher D. A., "J. Approvim. Theory", 1972, v. 6, № 2, p. 123-34; [17] Кahane J. P., там же, 1975, v. 13, p. 229-34; [18] Лин В. Я.,"Функц. анализ и его прилож.", 1976, т. 10, Л" 1, с. 37-45; [19] Витушкин А. Г., "Enseign. math.", 1977, t. 23, p. 255-320.

Л. Д. Кудрявцев.