Akademik

функция Скулема, сколемовская функция, - понятие логики предикатов. Если А( х ₁ ,. . . , х _n, у).предикатная формула от индивидных переменных х ₁,... , x_n, у, области изменения к-рых суть множества Х ₁, . . . , Х _п, Y соответственно, то функция f : Х ₁ Х. . .X X Х _пYназ. функцией Сколема, или разрешающей функцией, для формулы 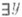( х ₁, . . . , х _п, у), если для всех имеет место импликация

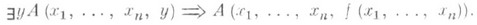
С. ф. были введены Т. Сколемом (Т. Skolem) в 20-х гг. 20 в. Понятие С. ф. широко применяется в работах по математич. логике. Объясняется это тем, что с помощью С. ф. можно исключить чередование кванторов " ^и $. Так, напр., для всякой формулы Аязыка узкого исчисления предикатов можно построить формулу вида $ x₁ ,. . . , х _п" y₁ ,..., у _т С, называемую сколемовской нормальной формой формулы А, где Сне содержит кванторов, но содержит новые (т. е. не встречающиеся в А).предикатные символы, и такую, что в исчислении предикатов формула Авыводима тогда и только тогда, когда выводима ее сколемовская нормальная форма.

Идея С. ф. используется в таких фундаментальных теоремах математич. логики, как теорема Эрбрана, сводящая вопрос о выводимости в исчислении предикатов предикатной формулы к исследованию вопроса о выводимости в исчислении высказываний бесконечной последовательности пропозициональных формул, теорема Лёвенхейма - Сколема и др.

В тех случаях, когда предметная область, на к-рой рассматриваются формулы, обладает дополнительной структурой, можно потребовать от С. ф. определенной связи с этой структурой. Напр., если рассматриваемая предметная область принадлежит иерархии конструктивных по Гёделю множеств, то можно потребовать, чтобы С. ф. также принадлежали определенному уровню в конструктивной иерархии. Существование С. ф., удовлетворяющих дополнительным свойствам, не всегда гарантировано, но эффект от их использования в случае, когда они существуют, оказывается более значительным.

В качестве примера можно указать на результат Йенсена о выводимости гипотезы Чэна о двух кардиналах (см. [6]) и отрицания Суслипа гипотезы (см. [5]) из аксиомы конструктивности Гёделя. Теорема Новикова - Кондо об униформизации 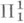-отношений из дескриптивной теории множеств утверждает существование определенного рода С. ф. (см. [2], с. 280).

Лит.:[1] Новиков П. С., Элементы математической логики, 2 изд., М., 1973; [2] Шенфилд Дж. Р., Математическая логика, пер. с англ., М., 1975; [3] Кейслер Г., Чэн Ч. Ч., Теория моделей, пер. с англ., М., 1977; [4] Ершов Ю. Л.

Палютин Е. А., Математическая логика М.. 1979; [5] Handbook of mathematical logic, Amst., 1977; [6] Dev1in K. J.,.Aspects of constnietibility, В. - [а. о.], 1973. В. Н. Гришин.