Akademik

алгебра 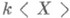многочленов (со свободными членами) над полем k от некоммутирующих переменных X. Свойство универсальности определяет алгебру 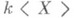единственным с точностью до изоморфизма образом: существует отображение 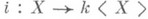такое, что любое отображение Xв нек-рую ассоциативную алгебру Ас единицей над k можно единственным образом пропустить через отображение i. Основные свойства алгебры :

1) алгебра 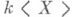вложима в тело (теорема Мальцева - Неймана);

2) алгебра обладает слабым алгоритмом деления, т. е. из соотношения

где , все , не равны нулю, , всегда следует, что существуют целое число 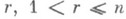, и элементы с ₁,. . .,с _r_₁ такие, что

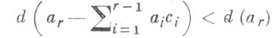
и (здесь d(a) - обычная степень многочлена ; ,

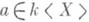3) алгебра 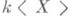является левым (правым) кольцом свободных идеалов (т. е. любой левый (правый) идеал алгебры 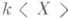является свободным модулем однозначно определенного ранга);

4) централизатор любого нескалярного элемента алгебры 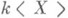(т. е . множество элементов, перестановочных с данным) изоморфен алгебре многочленов над kот одного переменного (т е о р е м а Б е р г м а н а).

Лит.:[1] К о н П., Универсальная алгебра, пер. с англ., М., 1968; [2] е г о ж е, Свободные кольца и их связи, пер. с англ., М., 1975. Л. А. Бокутъ.