Akademik

на дифференцируемом многообразии М- векторное поле Wна касательном пространстве ТМ, имеющее в терминах локальных координат ( х ¹,. .., х ^п, v¹,. . ., vⁿ).на ТМ, естественным образом связанных с локальными координатами ( х ¹,. .., х ^п).на М, компоненты (v¹,. . ., vⁿ, f¹,. .., fⁿ), где fⁱ=fⁱ(x¹,. . ., х ⁿ, v¹,. . . , vⁿ).- функции класса С ¹, причем при фиксированных х ¹,. . ., х ^п они являются положительно однородными функциями от v¹,. . ., vⁿ степени 2 (эти свойства Wне зависят от конкретного выбора локальных координат). Определяемая этим полем система дифференциальных уравнений

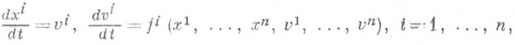
эквивалентна системе дифференциальных уравнений 2-го порядка

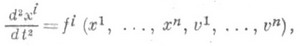
поэтому П. описывает (причем инвариантным образом, т. е. не зависящим от системы координат) систему таких уравнений на М.

Важнейший случай П.- когда fⁱ суть многочлены 2-й степени от vⁱ:

(*)

В этом случае 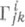задают на М аффинную связность с нулевым тензором кручения. Обратно, для всякой аффинной связности уравнения геодезич. линий задаются нек-рой П. с fⁱ вида (*) (причем при переходе от связности к пульверизации симметризуются по нижним индексам). Если поле W - класса С ², то fⁱ обязаны иметь вид (*). В общем случае W, каким бы гладким оно ни было вне нулевого сечения расслоения ТМ, не обязано быть полем класса С ² возле этого сечения. В такой ситуации иногда говорят об обобщенной П., оставляя термин "П." только для специального случая (*). Дифференциальные уравнения для геодезических в финслеровой геометрии приводят к обобщенной П. Можно дать определение П. в инвариантных терминах, пригодное и для банаховых многообразий (см. [1]).

Лит.:[1] Ленг С., Введение в теорию дифференцируемых многообразий, пер. с англ., М., 1967. Д. В. Аносов.