Akademik

- априорное распределение, максимизирующее функцию риска в статистич. задаче принятия решения.

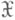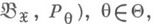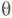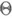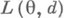Пусть по реализации случайной величины X, принимающей значения в выборочном пространстве (, надлежит принять решение dиз пространства решений при этом предполагается, что неизвестный параметр является случайной величиной, принимающей значения в выборочном пространстве (, ),. Пусть функция выражает потери, к-рые возникают при принятии решения d, если истинное значение параметра есть 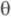. Априорное распределение из семейства наз. наименее благоприятным для решения dв статистической задаче принятия решения при бейесовском подходе, если

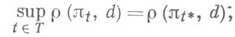
где

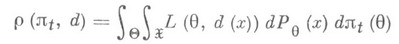
- функция риска, выражающая средние потери от принятия решения d.H. б. р.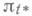позволяет вычислить самые "тяжелые" (в среднем) потери 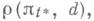возникающие при принятии решения d. В практич. деятельности ориентируются, как правило, не на Н. б. р., а наоборот, стараются принять такое решение, к-рое предохранило бы от максимальных потерь при изменении параметра в, что приводит к поиску минимаксного решения , минимизирующего максимальный риск, т. е.

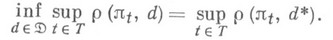
В задаче проверки сложной статистич. гипотезы против простой альтернативы при бейесовском подходе Н. б. р. определяется с помощью редукции Вальда, к-рая заключается в следующем. Пусть по реализации случайной величины Xнадлежит проверить сложную гипотезу 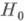, согласно к-рой закон распределения Xпринадлежит семейству 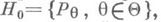против простой альтернативы , согласно к-рой случайная величина Xподчиняется закону Q, и пусть

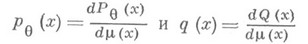
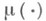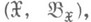
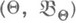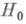где - нек-рая s-конечная мера на - семейство априорных распределений на . Тогда для любого сложной гипотезе можно сопоставить простую гипотезу 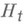, согласно к-рой случайная величина Xподчиняется вероятностному закону, имеющему плотность вероятности

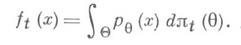
Согласно Неймана- Пирсона лемме для проверки простой гипотезы 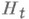против простой альтернативы 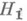существует наиболее мощный критерий, построенный на отношении правдоподобия. Пусть 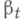- мощность этого критерия, тогда Н. б. р. есть то априорное распределение из семейства , для к-рого выполняется неравенство для всех 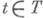. Н. б. р. обладает тем свойством, что плотность вероятности 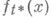случайной величины Xпри гипотезе 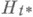"наименее удалена" от альтернативной плотности q(x), т. е. гипотеза является самой "близкой" из семейства 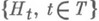к конкурирующей гипотезе Н ₁. См. Бейесовский подход. Лит.:.[1] Леман Э., Проверка статистических гипотез, пер. с англ., 2 изд., М., 1979; [2] 3акс Ш., Теория статистических выводов, пер. с англ., М., 1975. М. С. Никулин.