Akademik

распределение вероятностей какой-либо случайной величины, рассматриваемое в противоположность условному распределению этой случайной величины при нек-ром дополнительном условии. Обычно термин "А. р." употребляют в следующей обстановке. Пусть 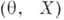- пара случайных величин (случайных векторов или более общих случайных элементов). Случайную величину 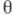рассматривают как неизвестный параметр, а X - как результат наблюдений, предназначенных для оценки 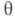. Совместное распределение задают распределением (которое п называют в этом случае А. р.) и совокупностью условных распределений 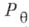случайной величины 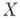по отношению к 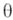. По Бейеса формуле можно вычислить условное распределение 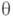относительно X(которое в этом случае называют апостериорным распределением 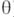). В статистпч. задачах часто А. р. неизвестно (и даже само предположение о его существовании не представляется достаточно обоснованным). Об использовании А. р. см. Бейесовский подход.

Ю. В. Прохоров.