Akademik

функция, обратная к показательной функции. Л. ф. обозначается

ее значение у, соответствующее значению аргумента х, наз. натуральным логарифмом числа х. В силу определения соотношение (1) равносильно

Так как 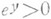при любом действительном у, то Л. ф.

определена только при x>0. В более общем смысле

Л. ф. наз. функцию

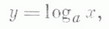
где - произвольное основание логарифмов; эта функция выражается через ln хпо формуле:

где M=1/ln a. Л. ф.- одна из основных элементарных функций; ее график (см. рис.) носит название л о г а р и ф м и к и. Основные свойства Л. ф. вытекают из соответствующих свойств показательной функции и логарифмов; напр., Л. ф. удовлетворяет функциональному уравнению

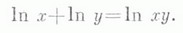
Л. ф. y=ln хявляется строго возрастающей функцией, причем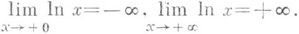

В каждой точке x>0 Л. ф. имеет производные всех порядков и в достаточно малой ее окрестности раскладывается в степенной ряд, т. е. является аналитической функцией.

Для 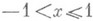справедливо разложение Л. ф. в степенной ряд:

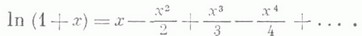
Производная Л. ф.:

Многие интегралы выражаются через Л. ф.; напр.:

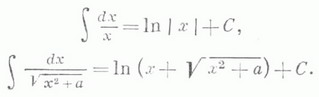
Впервые зависимость между переменными величинами, выражаемая Л. ф., рассматривалась Дж. Непером (J. Napier, 1614).

Л. ф. на комплексной плоскости является многозначной (бесконечнозначной) функцией, определенной при всех значениях аргумента 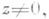и обозначается ln z. Однозначная ветвь 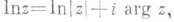этой функции, определяемая как

где arg z - главное значение аргумента комплексного числа z, носит название главного значения Л. ф. Имеем

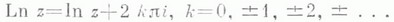
Все значения Л. ф. для отрицательных действительных z являются комплексными числами. Первая удовлетворительная теория Л. ф. в комплексной плоскости была дана Л. Эйлером (L.Euler, 1749), к-рый исходил из определения

Лит.: [1] Н и к о л ь с к и й С. М., Курс математического анализа, 2 изд., т. 1, М., 1975: [2] М а р к у ш е в и ч А. И., Теория аналитических функций. 2 изд., т. 1, М., 1967. БСЭ-3.