Akademik

методы комплексного переменного - методы изучения К. з. для дифференциальных уравнений с частными производными, в к-рых используется представление решений через аналитич. функции комплексного переменного.

Пусть для уравнения 2-го порядка эллиптич. типа

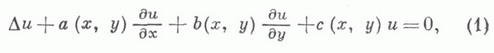
где а, Ь, с - аналитич. функции действительных переменных х, у внек-рой области плоскости 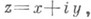поставлена К. з.: найти регулярное в односвязной области решение уравнения (1), удовлетворяющее краевому условию

где 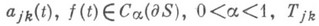- линейные операторы, отображающие 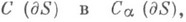причем 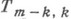- вполне непрерывны. Эта задача охватывает известные классические краевые задачи Дирихле, Неймана, Пуанкаре и др. При помощи формулы общего представления решений (см. Дифференциальное уравнение с частными производными;. методы комплексного переменного):

эта задача приводится к эквивалентной К. з. для аналитич. функций:

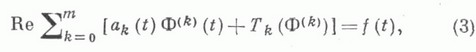
где 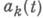- заданные непрерывные в смысле Гёльдера функции, - вполне непрерывный оператор, а - линейные операторы. Пусть конечная односвязная область Sограничена замкнутым контуром Ляпунова (см. Ляпунова поверхности и кривые) 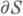и пусть производная порядка голоморфной в Sфункции Ф (г) принимает на 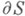значения функции класса 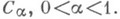Тогда, считая, что точка z=0 принадлежит S, функцию Ф(z) представляют в виде:

где m(t) - действительная функция класса 0<a<1, а с - действительная постоянная; и с определяются по Ф (z) единственным образом. Подстановка этих выражений в краевое условие (3) позволяет получить для искомой функции эквивалентное задаче (2) сингулярное интегральное уравнение вида

где Т - вполне непрерывный оператор. Для нормальной разрешимости К. з. (2) необходимо и достаточно, чтобы

Задача Дирихле (m=0) всегда нормально разрешима. (Ниже всюду предполагается, что условие (4) соблюдено. Индекс К. з. (2) вычисляется по формуле

где р - приращение функции 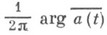при однократном обходе контура 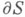в положительном направлении. Индекс задачи Дирихле равен нулю. Однородная К. з. 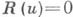имеет конечное число 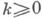линейно независимых решений, причем а неоднородная задача (2) имеет решение тогда и только тогда, когда выполняются равенства

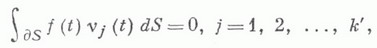
где - полная система линейно независимых решений союзного однородного интегрального уравнения

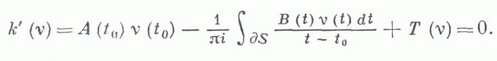
Необходимым и достаточным условием для того, чтобы К. з. (2) имела решение для любой правой части, является наличие ровно 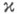линейно независимых решений у соответствующей однородной задачи R(u)=0. Следовательно, в случае 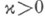однородная К. з. R(u)=0 всегда имеет не меньше, чем х, линейно независимых решений, а при неоднородная задача (2) не допускает решения для любой правой части, причем число условий разрешимости не меньше

Необходимые и достаточные условия разрешимости неоднородной К. з. могут быть сформулированы в терминах замкнутости относительно рассматриваемой области нек-рого ядра, а также полноты определенной системы функций. Эти ядра и системы функций строятся в явном виде при помощи функции Римана уравнения (1) и коэффициентов краевого условия. Напр., пусть 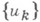- некоторая полная система решений относительно основной области D₀ уравнения (1) и пусть 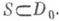Тогда необходимым и достаточным условием разрешимости задачи (2) для любой правой части является полнота системы функций {R(u_k)}на границе.

Весьма полные результаты получены относительно следующей К. з. (обобщенной задачи Римана - Гильберта): найти решение уравнения

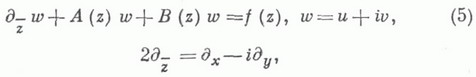
непрерывное в 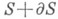и удовлетворяющее краевому условию

где 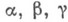- заданные действительные функции, принадлежащие классу 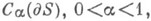причем Область S, вообще говоря, многосвязна. Такая задача может быть редуцирована к эквивалентному сингулярному интегральному уравнению. Этим путем удается получить полный качественный анализ К. з. (6).

Пусть граница 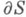области Sсостоит из конечного числа простых замкнутых кривых удовлетворяющих условиям Ляпунова. Так как при конформных отображениях вид уравнения и краевого условия сохраняются, то без ущерба для общности можно считать, что 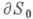- единичная окружность с центром в точке z=0, лежащей в рассматриваемой области - окружности, лежащие внутри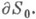

Индексом задачи (6) наз. целое число п, равное приращению когда точка z один раз обойдет 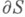в положительном направлении. Краевое условие можно привести к более простому виду

где причем 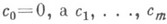- некоторые действительные постоянные, к-рые однозначно выражаются через a и b. Индекс сопряженной задачи

вычисляется по формуле:n'=-n+m-1.

Задача (6) имеет решение тогда и только тогда, когда

где w* - произвольное решение сопряженной задачи. Пусть еи е' - числа линейно независимых решений однородных задач (6) и (7) соответственно. Тогда

Если n<0, то однородная задача (6) не имеет нетривиальных решений. Если n>m-1, то однородная задача (6) имеет ровно е=2п+1-т линейно независимых решений, а неоднородная задача (6) всегда разрешима. Если n<0, то неоднородная задача (6) имеет решение тогда и только тогда, когда

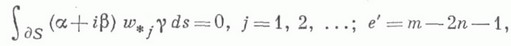
где 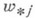- полная система решений однородной задачи (7). Если m=0 и n=0, то е=1 и все решения однородной задачи [6] имеют вид

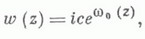
где с - действительная постоянная, а w₀ - непрерывная в 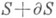функция. Приведенные результаты полностью характеризуют задачу в односвязном (m=0) и многосвязном (n<0, n>m-1) случаях. Особого рассмотрения требуют случаи к-рые также в достаточной мере детально разработаны. Для уравнения (5) изучена также К. з. типа Пуанкаре задачи.

Лит. см. при ст. Дифференциальное уравнение с частными производными;методы комплексного переменного. И. Н. Векуа.