Akademik

топологическая группа, являющаяся проективным пределом системы конечных групп , снабженных дискретной топологией (I - предупорядоченное множество). П. г. Gобозначается 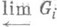. Как подпространство прямого произведения , снабженного компактной топологией (базой окрестностей единицы является система ядер проекций ), она замкнута и потому компактна.

Примеры. 1) Пусть I - множество целых чисел, больших нуля, с естественным отношением порядка и . Пусть - естественный эпиморфизм и

для любых i<j. Тогда -(аддитивная) группа кольца целых р-адических чисел.

2) Всякая компактная аналитич. руппа над полем р-адических чисел (напр., 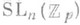) является (как топологич. группа) П. г.

3) Пусть G - абстрактная группа и - семейство всех ее нормальных делителей конечного индекса. На I можно ввести отношение , положив , если . Это отношение превращает I в предупорядоченное множество. Сопоставляя каждому группу G/H_i и каждой паре из I - естественный гомоморфизм , получают П. г. 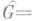, наз. ассоциированной с GП. г.; она является отделимым пополнением группы Gотносительно топологии, определенной подгруппами конечного индекса. Ядро естественного гомоморфизма является пересечением всех подгрупп конечного индекса. В этой конструкции можно было бы вместо семейства всех нормальных делителей конечного индекса рассматривать лишь те, индекс к-рых есть степень фиксированного простого числа р. Соответствующая группа обозначается и является про-р-группой.

4) П. г. следующим образом естественно возникают в теории Галуа (вообще говоря, бесконечных) алгебраич. расширений полей. Пусть K/k - Галуа расширение и - семейство всех конечных расширений Галуа поля k, лежащих в К. Тогда . На I можно ввести отношение , положив , если . Тогда I становится предупорядоченным множеством. Пусть GalK_i/k- группа Галуа расширений K_i/k. Каждой паре из I сопоставляется естественный гомоморфизм

Тогда соответствующая П. г. (абстрактно) изоморфна группе Gal K/k, что позволяет считать Gal K/k П. г. Система подгрупп Gal K/K_i образует в Gal K/k систему окрестностей единицы (см. Галуа топологическая группа). Эта конструкция получает обобщение в алгебраич. геометрии при определении фундаментальной группы схемы. П. г. могут быть охарактеризованы как компактные вполне несвязные группы (см. Компактная группа), а также как компактные группы, у к-рых имеется множество открытых нормальных делителей, образующее систему окрестностей единицы. Теория когомологий П. г. (см. Когомологии групп, Галуа когомологий).играет важную роль в современной теории Галуа.

Лит.:[1] Серр Ж.-П., Когомологии Галуа, пер. с франц., М., 1068; [2] Кох X., Теория Галуа р-расширений, пер. с нем., М., 1973; [3] Алгебраическая теория чисел, пер. с англ., М., 1969. В. Л. Попов.