Akademik

- метод решения системы линейных алгебраич. уравнений А х= b с эрмитовой невырожденной матрицей А. Среди прямых методов он наиболее эффективен при реализации на ЭВМ.

Вычислительная схема метода в общем случае основана на факторизации эрмитовой матрицы Ав виде

где S- правая треугольная матрица с действительными положительными диагональными элементами, D- диагональная матрица с элементами 1 пли -1 на диагонали. Из (1) непосредственно получаются рекуррентные соотношения для вычисления элементов s_ij и d_ii матриц Sи D:

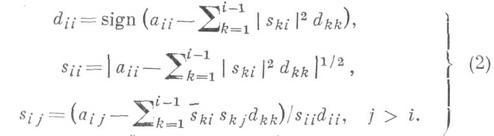
После того как факторизация (1) выполнена, решение исходной системы сводится к последовательному решению двух систем S*Dy=b и Sx=y с треугольными матрицами. В этой части К. к. м. совпадает с обратным ходом большинства прямых методов решения систем (см. Гаусса метод).

В действительном случае, когда А- симметрич. матрица, схема (2) соответствует разложению A = S'DS с действительной матрицей Sи несколько упрощается. Существенное упрощение схемы (2) происходит, когда А- положительно определенная матрица. В этом случае D = E, A = S*S.

Известны схемы К. к. м. для неположительно определенных матриц, основанные на факторизации вида A=S*S. Для вычисления элементов Sимеют место рекуррентные соотношения, аналогичные (2). Однако эта факторизация не эффективна для реализации на ЭВМ в случае, когда А- действительная матрица, так как при вычислении матрицы Sвозможен выход в комплексную арифметику.

Из характеристик К. к. м. важны следующие.

1) Среди прямых методов решения систем, основанных на факторизации матрицы, К. к. м. обладает самым высоким быстродействием (в два раза выше, чем у метода Гаусса).

2) Для факторизации матрицы по К. к. м. достаточно задавать компактную информацию о матрице в виде элементов ее треугольной половины. Кроме того, схема (2) позволяет записывать в память ЭВМ матрицу Sна месте исходной информации об А. Это существенно увеличивает порядок решаемых систем.

3) Вычислительная схема К. к. м. допускает сегментированную обработку исходной матрицы участками из нескольких последовательных строк. Использование внешней памяти при этом позволяет решать системы высокого порядка.

4) К. к. м. сохраняет ленточную структуру матрицы, т. е. матрица Sбудет иметь тот же вид, что и верхняя половина исходной матрицы.

5) Особенно эффективен К. к. м. для систем с положительно определенными матрицами. В данном случае нет роста элементов матрицы в процессе вычислений. Это свойство обеспечивает устойчивость вычислительного процесса к ошибкам округления. Мажорантная оценка точности вычисленного решения в этом случае - минимальная в классе прямых методов. Понижению общего уровня ошибок способствует и возможность вычисления скалярного произведения векторов в схеме (2) в режиме накопления с удвоенной точностью.

Отсутствие роста элементов в процессе вычислений делает удобным реализацию К. к. м. на ЭВМ, работающих в арифметике с фиксированной запятой.

6) Разложение (1) по К. к. м. может быть использовано для вычисления определителя матрицы, обращения матрицы.

Лит.:[1] Воеводин В. В., Численные методы алгебры, М., 1966; [2] Бахвалов Н. С, Численные методы, М 1974; [4] Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ., М., 1970; [4] Воеводин В. В., Вычислительные основы линейной алгебры, М., 1977.

Г. Д. Ким.