Akademik

в теории графов - разложение графа на непересекающиеся по ребрам остовные подграфы специального вида. В общем случае фактор есть остовный подграф, обладающий заданным свойством. Примером такого свойства является регулярность подграфа. Регулярный остовный подграф степени kназ. k-фактором; 1-фактор наз. также совершенным паросочетанием. Граф наз. k- факторизуемым, если он может быть представлен как объединение своих непересекающихся по ребрам k-факторов.
В теории графов рассматриваются вопросы о существовании факторов того или иного вида в произвольном графе, о числе факторов, о возможности Ф. данного типа для различных классов графов. Известно, напр., что полный граф с четным числом вершин и полный граф двудольный с одинаковым числом вершин в каждой доле являются 1-факторизуемыми. Связный граф является 2-факторизуемым тогда и только тогда, когда он является регулярным графом четной степени. Граф Gимеет 1-фактор тогда и только тогда, когда число его вершин четно и не существует такого подмножества вершин U, что число компонент связности с нечетным числом вершин графа G - U, получающегося из G удалением вершин множества U, превышает |U|. Всякий двусвязвый регулярный граф степени 3 может быть разложен на непересекающиеся 1-фактор и 2-фактор.
Примерами нерегулярных факторов являются ос-товные деревья и леса, остовные плоские подграфы (см. Графа укладка )и т. п. С разложением графа на остовные леса связана числовая характеристика, называемая древесностью,- это наименьшее число непересекающихся по ребрам остовных лесов, объединением к-рых является граф. Древесность произвольного графа Gравна

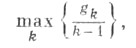
где g_k - наибольшее число ребер в k-вершинныx подграфах графа G.

Лит.:[1] Xарари Ф., Теория графов, пер. с англ., М., 1973.
А. А. Сапоженко.