Akademik

- 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п - алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения f(x)=0 в результате решения более простых уравнений, степеней не больших п. Иногда Р. называют само рациональное выражение

Пусть f(x) - сепарабельный многочлен над полем kс группой Галуа Gи H - нормальный делитель группы G. Пусть - рациональное выражение от x₁, . .., х _п, остающееся инвариантным при всех подстановках корней х ₁, . . ., х _п из группы Н, и Тогда уявляется корнем нек-рого уравнения g(y) =0с коэффициентами из k, группа Галуа к-рого является собственной факторгруппой группы G. Таким образом, решение уравнения f(x)=0 сводится к решению уравнения g(y)=0 и решению уравнения f(x)=0 над полем k(y₁, ..., y_s).

Напр., для решения уравнения 4-й степени

(любое уравнение 4-й степени приводится к такому виду) используют кубич. Р.

корни к-рой y₁, y₂, y₃ связаны с корнями х ₁, x₂, х ₃, x₄ соотношениями.. Корни y₁, y₂, y₃ определяются с помощью формулы Кардано, что позволяет определить и корни х ₁, х₂, x₃, x,₄.

Последовательное применение метода Р. позволяет свести решение любого уравнения с разрешимой группой Галуа к решению цепочки уравнений с циклич. группой Галуа. Для решения последних используются резольвенты Лагранжа.

Пусть f(х)=0 - уравнение над полем kс циклич. группой Галуа G порядка пи пусть kсодержит первообразный корень из единицы степени п. Для элемента a, принадлежащего нолю разложения многочлена f(x), и характера c группы G в группу корней из единицы степени n р е з о л ь в е н т а Лагранжа r (c, a) определяется формулой

(*)

Пусть a=x₁- один из корней многочлена f(х)и c пробегает все характеры группы G. Тогда система линейных уравнений (*) позволяет определить корни x₁, x₂,. . ., х _п, если известны резольвенты Лагранжа для всех характеров c группы G. Для выполняется соотношение

к-рое показывает, что элементы при любом целом iинвариантны относительно G и, следовательно, являются однозначно определенными рациональными выражениями от коэффициентов многочлена f (х)и корня . Если c порождает группу характеров группы G, то имеют место равенства и для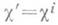

Р е з о л ь в е н т о й Г а л у а уравнения f(x)=0наз. такое неприводимое над данным полем алгебраич. уравнение у(х)=0(см. Галуа теория), что в результате присоединения одного из его корней к этому полю получается поле, содержащее все корни уравнения f(x)= 0.

Лит.:[1] В а н д е р В а р д е н Б. Л., Алгебра, пер. с нем., 2 изд., М., 1979. Л. В. Кузьмин.

2) В теории интегральных уравнений под Р. (разрешающим ядром) уравнения

(**)

понимают функцию Г (s, t;l) переменных s, tи параметра l, при помощи к-рой решение уравнения (**) представляют в виде

если l, не есть собственное значение уравнения (**), напр. для ядра K(s, t)=s+t резольвентой является функция

БСЭ-3.

3) Р. о п е р а т о р а - оператор Rl, обратный к Т _l = =А-l Т, где А - замкнутый линейный оператор, определенный на плотном множестве D_A банахова пространства Xсо значениями в том же пространстве, при условии, что l, таково, что есть линейный непрерывный оператор, определенный на всем X. Точки l, для к-рых Р. существует, наз. р е г у л я р н ы м и т о чк а м и оператора А , а совокупность всех регулярных точек - р е з о л ь в е н т н ы м м н о ж е с т в о м r(A) этого оператора. Множество r(А)- открытое и на каждой его связной компоненте оператора R_l, является аналитич. цией параметра l. Свойства Р.:

1) для любых двух точек l,

2)

из R_l х=0следует x=0;

3) если X - гильбертово пространство, то

Лит.:[1] И о с и д а К., Функциональный анализ, пер. с англ., М., 1967; [2] А х и е з е р Н. И., Г л а з м а н И. М., Теория линейных операторов в гильбертовом пространстве, 2 изд., М., 1966; [3] К а н т о р о в и ч Л. В., А к и л о в Г. П., Функциональный анализ, 2 изд., М., 1977. В. И. Соболев.

4) В гомологической алгебре Р. м о д у л я - комплекс С, определенный для положительных степеней и снабженный пополняющим гомоморфизмом (модуль Арассматривается как комплекс, равный нулю в ненулевых степенях) таким образом, что последовательность точна. Р. наз. инъективной, если все С ⁱ инъективны. Двойственным образом определяется проективная резольвента. Р. является основным средством вычисления производных функторов. В частных случаях удобно использовать специальные виды Р. Напр., для кольца многочленов внешняя алгебра превращается в Р. тривиального R-модуля k, если задать дифференциал и пополняющий гомоморфизм . Эта конструкция применима к кольцам степенных рядов (как сходящихся, так и формальных) и носит название к о м п л е к с а К о з ю л я.

В. Е. Говоров.