Akademik

полная кривизна, поверхности - произведение главных кривизн регулярной поверхности в данной точке.

Если

- первая квадратичная форма поверхности и

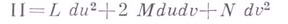
- вторая квадратичная форма поверхности, то Г. к. вычисляется по формуле

Г. к. совпадает с якобианом сферического отображения.

где 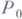- точка на поверхности, s - площадь области U, содержащей , S - площадь сферич. изображения U, d- диаметр области. Г. к. положительна в эллиптической точке, отрицательна в гиперболической точке и равна нулю в параболической точке и в уплощения точке. Г. к. можно выразить только через коэффициенты первой квадратичной формы и их производные (см. Гаусса теорема). Именно,

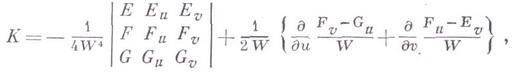
где

Так как Г. к. зависит только от метрики, т. е. от коэффициентов первой квадратичной формы, то Г. к.- инвариант изгибания. Г. к. играет особую роль в теории поверхностей; существует много формул для ее вычисления (см., напр., [2]).

Г. к. наз. гауссовой кривизной по имени К. Гаусса, к-рый ввел это понятие (см. [1]).

Лит.:[1] Гаусс К. Ф., Общие исследования о кривых поверхностях, пер. с лат., в сб.: Об основаниях геометрии, М., 1956; [2] Бляшке В., Введение в дифференциальную геометрию, пер. с нем., 1957, с. 95. Е. В. Шикин.