Akademik

(theorema egregium): гауссова кривизна (произведение главных кривизн) регулярной поверхности в евклидовом пространстве 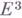не меняется при изгибаниях поверхности. (Здесь регулярность означает 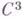-гладкое погружение.) Г. т. следует из того, что гауссова кривизна Кповерхности в точке 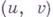может быть выражена через коэффициенты первой квадратичной формы поверхности

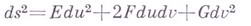
и их первые и вторые производные в этой точке. Такое выражение для Кназ. уравнением Гаусса, оно допускает разные формы записи (см., напр., [2]). Запись уравнения Гаусса упрощается при специализации координат. Так в изотермич. координатах ( ):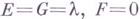

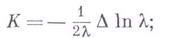
в полугеодезич. координатах ( ):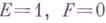

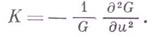
Уравнение Гаусса вместе с Петерсона- Кодацци уравнениями образуют условия интегрируемости системы, к к-рой сводится задача восстановления поверхности по ее первой и второй квадратичным формам. Из Г. т. и Гаусса - Бонне теоремы следует, что отличие суммы углов геодезич. треугольника на регулярной поверхности от л равно ориентированной площади сфе-рич. образа этого треугольника (см. [1]).

Г. т. установлена К. Гауссом (С. Gauss) в [1] и является первым и важнейшим результатом в исследовании связей между внутренней и внешней геометриями поверхностей.

Для регулярной m-мерной, , поверхности F^m в римановом пространстве F^m справедливо следующее обобщение Г. т. (см. [3], с. 125; [4], с. 195):

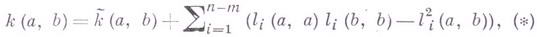
где 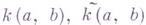кривизны соответственно 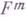и 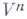в двумерном направлении, определяемом касательными к 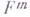в рассматриваемой точке векторами 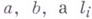- вторая квадратичная форма относительно г-й нормали из ортонормированного набора нормалей в этой точке. Из (*) следует, что для гиперповерхности 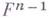в все четные элементарные симметрические функции главных кривизн

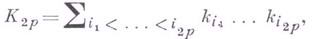
определяются внутренней метрикой 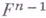В четномерном 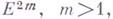гиперповерхность 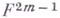однозначно определяется ее внутренней метрикой и кривизной Гаусса - Кронекера:

при условии, что последняя отлична от нуля (см. [5], с. 288).

Для широких классов двумерных нерегулярных поверхностей в 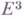удается определить "внешнюю кривизну" как борелевскую меру, связанную со сферич. отображением, и "внутреннюю кривизну" как меру, связанную с отличием суммы углов треугольников от я. Обобщение Г. т. состоит в утверждении, что внешняя и внутренняя кривизны совпадают. Такое обобщение Г. т. получено для общих выпуклых поверхностей (см. (6]) и для С ¹ -гладких поверхностей ограниченной внешней кривизны (см. [7]).

Лит.:[1] Гаусс К. Ф., Общие исследования о кривых поверхностях, пер. с лат., в сб.: Об основаниях геометрии, М., 1956; [2] Бляшке В., Введение в дифференциальную геометрию, пер. с нем., М., 1957; [3] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [4] Эйзенхарт Л. П., Риманова геометрия, пер. с англ., М., 1948; [5] Стериберг С., Лекции по дифференциальной геометрии, пер. с англ., М., 1970; [61 Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М.- Л., 1948; [7] Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969. Ю. Д. Бураго.