Akademik

ENTROPIE

La notion d’entropie, sa définition et le terme lui-même furent introduits dans la thermodynamique en 1854, par le physicien allemand Rudolf Clausius (1822-1888). En fait l’événement doit être considéré comme la naissance même de cette discipline consacrée à l’étude macroscopique des processus d’évolution au sein des milieux hautement complexes à l’échelle moléculaire. Comme devait l’observer plus tard son contemporain américain, le physicien Willard Gibbs (1839-1903), cette contribution marque une époque dans l’histoire de la physique.

L’intervention d’une fonction d’état appelée énergie , (du grec 﨎益﨎福塚礼﨟, cause de travail), avait déjà permis une formulation du premier principe de la thermodynamique, moins anthropocentrique que celle de l’impossibilité d’un mouvement perpétuel sans contrepartie. Semblablement, la découverte d’une autre fonction d’état, dénommée entropie (du grec, 﨎益精福礼神兀, cause d’évolution) a permis d’opérer de même avec le second principe, fondé depuis les travaux de Sadi Carnot (1796-1832) sur l’impossibilité du mouvement perpétuel dit de deuxième espèce (1824) [cf. THERMODYNAMIQUE].

Toutefois, si le concept d’énergie, dérivé d’une propriété essentiellement quantitative de conservation, a été facilement accueilli comme une notion première et rapidement vulgarisée, il n’en a pas été de même pour celui d’entropie jugé souvent obscur en raison de son contenu plus qualitatif, de désordre, de désorganisation et d’irréversibilité. Dès lors, son interprétation nécessite une analyse attentive, tant au point de vue macroscopique adopté par Clausius que microscopique considéré ultérieurement par Ludwig Boltzmann (1844-1906) et ses successeurs.

Définition macroscopique

En prenant pour base le second principe de la thermodynamique selon lequel: Il est impossible de décrire un cycle moteur au moyen d’une seule source de chaleur , le physicien anglais W. Thomson (lord Kelvin, 1824-1907) en a déduit l’échelle thermodynamique absolue de température T. Celle-ci a été utilisée peu après par Clausius, pour formuler son théorème fondamental:

Dans cette relation, l’intégration est étendue à un cycle, autrement dit à une transformation dont l’état final est confondu avec son état initial. D’autre part, la quantité d Q représente l’élément de chaleur reçu (d Q 礪 0) ou fourni (d Q 麗 0) par le milieu considéré au moment où il possède la température T, supposée uniforme. En fait, le théorème de Clausius exprime en puissance tout le contenu du second principe; il peut d’ailleurs être étendu sans difficulté aux milieux à température non uniforme.

En particulier, le signe d’égalité concerne les cycles réversibles qui sont des successions d’états d’équilibre ^{[cf. IRRÉVERSIBILITÉ]}. Il en résulte que, dans le domaine des processus réversibles, l’intégrale de l’élément d Q/T entre deux états A et B est indépendante du chemin ACB adopté. Cette indépendance est le propre d’une fonction d’état, ce qui permet d’écrire:

où la grandeur S, ainsi définie à une constante arbitraire près, a été appelée par Clausius l’entropie du milieu considéré. La même propriété écrite sous la forme différentielle: d S = d Q/T permet d’interpréter la température absolue T comme un diviseur intégrant de l’élément de chaleur exprimé en fonction des variables d’état du système.

Dans le cas d’une transformation ACB irréversible, le même raisonnement conduit à l’inégalité:

Toutefois, ce résultat implique l’existence d’au moins un chemin réversible entre les états A et B, ce qui signifie que ces derniers sont eux-mêmes des états d’équilibre. Une extension plus complète de la définition de l’entropie aux états de non-équilibre est fournie à partir de l’analyse microscopique exposée au dernier chapitre.

Auparavant, les quelques propriétés suivantes peuvent être dégagées de l’inégalité fondamentale Td S 閭 d Q:

– L’entropie est une variable extensive, ce qui signifie notamment qu’elle est la somme des entropies de chacune des parties dont le système est composé.

– La constante arbitraire subsistant dans la définition peut être prise égale à zéro en vertu du principe de W. Nernst (1864-1921), selon lequel l’entropie de tous les corps critallisés est la même au zéro absolu de température. – L’évolution de tout milieu isolé (d Q = 0, transformation adiabatique) s’accompagne nécessairement d’un accroissement d’entropie et tend vers un état d’équilibre qui correspond à l’entropie maximale (d S = 0 à l’équilibre). Ce dernier est généralement caractérisé par une uniformisation qui témoigne d’un état de dégradation complète. Il s’ensuit la propriété fondamentale de l’entropie d’être une mesure de désordre, ce que confirme l’analyse microscopique.

– L’introduction de l’entropie dans l’expression du second principe de la thermodynamique permet d’écrire ce dernier sous la forme d’un bilan, représenté symboliquement par l’égalité:

Le premier terme du membre de droite désigne le flux entropique , dû à la contribution du milieu extérieur sous forme de flux de conduction et de convection; son signe n’est généralement pas défini. Le second terme représente l’ensemble des effets dissipatifs engendrés par les processus irréversibles internes; il porte le nom de production d’entropie ; ici le signe est essentiellement défini positif, et traduit la condition imposée à toute évolution par le second principe. – Dans le cadre plus restreint du seul domaine des états d’équilibre et des transformations réversibles, l’introduction de la notion d’entropie peut être obtenue par d’autres voies. Parmi celles-ci, la recherche d’un diviseur intégrant de l’élément de chaleur, évoquée plus haut, et la méthode de Carathéodory (1909), sont les plus connues. – Au point de vue des applications, l’emploi de l’entropie comme variable d’état a suscité un large développement dans l’usage des représentations graphiques des processus thermodynamiques. Il en est ainsi notamment des diagrammes température-entropie de Stodola (cf. figure) enthalpie-entropie de Mollier, et plus généralement encore des surfaces thermodynamiques de J. W. Gibbs, ^{[cf. THERMODYNAMIQUE]}.

Définition microscopique

Le physicien viennois Ludwig Boltzmann (1844-1906) fut le premier à proposer une interprétation microscopique de la notion d’entropie. Dès 1877, il reliait celle-ci à une mesure du désordre moléculaire par l’importante relation devenue classique:

où intervient la constante universelle, dite aussi constante de Boltzmann, k = 1,38 憐 10^-23 en unités S.I. (joule par degré Kelvin). D’autre part, la quantité W représente, pour un état macroscopique donné, le nombre correspondant des états microscopiques – ou micro-états – qui permettent de le réaliser. En particulier, l’état macroscopique d’une masse donnée de gaz, défini par exemple à l’aide des variables de température et de pression, peut être réalisé par un nombre considérable de combinaisons distinctes de groupements moléculaires dénommées complexions . La quantité W correspond à ce nombre de complexions et est prise comme mesure de la probabilité thermodynamique de l’état macroscopique correspondant. Il faut cependant souligner que cette probabilité thermodynamique W (de l’allemand Wahrscheinlichkeit ), ne relève nullement de la définition habituelle d’une probabilité, puisque sa mesure n’est pas normée à l’unité.

La relation (1) conduit à une interprétation remarquable de la loi de croissance de l’entropie. Elle montre, en effet, qu’un système isolé évolue nécessairement et irréversiblement vers des états de plus en plus probables et de moins en moins ordonnés sous l’effet des chocs moléculaires, jusqu’à son état final d’équilibre qui est ainsi le plus probable.

Cette constatation conduit à une interprétation statistique du second principe de la thermodynamique, qui en limite la validité aux systèmes complexes, c’est-à-dire composés d’un grand nombre de paramètres moléculaires. Dans ce dernier cas, un processus hautement improbable, comme la séparation spontanée des deux constituants d’un mélange gazeux, s’interprète comme une impossibilité pratique.

Toutefois, la justification de la relation (1) et de ses conséquences soulève de nombreuses difficultés dès qu’on envisage des situations plus réalistes et moins simplistes que celles de micro-états, définis uniquement à partir des considérations de position, analogues à celles d’un ensemble de billes réparties entre deux boîtes.

Déjà, dans le cas du mouvement chaotique des molécules d’un gaz, soumises individuellement aux lois de la dynamique classique, la détermination du nombre de micro-états devient ambiguë. En effet, ce nombre est assimilable au volume de l’espace des phases 臨, accessible au système; mais comme il n’existe pas d’unité naturelle pour ce volume, l’entropie ne peut être définie qu’à une constante près. Max Planck a levé cette ambiguïté grâce à l’intervention de la mécanique quantique, où la notion du nombre de micro-états est définie sans équivoque ^{[cf. STATISTIQUE]}.

On sait que, en mécanique statistique, l’état d’un système dynamique est défini par une densité de probabilité dans le cas classique ou par une matrice densité dans le cas quantique. On en déduit respectivement pour l’entropie, l’expression de Gibbs dans l’espace des phases:

où Tr représente la trace de la matrice, c’est-à-dire la somme des éléments diagonaux. On remarque au passage la similitude entre cette expression et celle de C. Shannon (1949), ⁱ p ⁱ logp ⁱ , qui exprime le contenu d’information d’une distribution discrète de probabilité (cf. théorie de l’INFORMATION).

Malheureusement, les expressions (2) sont des invariants du mouvement; elles ne peuvent donc en aucun cas rendre compte de la croissance monotone de l’entropie qui est le propre des phénomènes dissipatifs au sein des systèmes isolés ^{[cf. STATISTIQUE]}. Pour remédier à cette situation, et en vue d’établir une théorie microscopique des processus irréversibles, on dispose de deux orientations. Toutefois, aucune d’entre elles n’est encore complètement satisfaisante bien que d’importants progrès aient été enregistrés en faveur de la seconde.

La première est la théorie cinétique utilisée initialement par Boltzmann, et selon laquelle on cherche à décrire l’évolution irréversible d’une partie 福⁰ de l’état statistique au moyen d’une fonctionnelle de 福⁰ possédant la propriété de croissance requise pour toute définition de l’entropie. Boltzmann en a déduit d’abord l’équation fermée qui porte son nom, dans le cas d’une distribution à une particule f (x , v, t ) relative à un gaz dilué. Il a établi ensuite le théorème connu universellement connu sous le nom de théorème H, impliquant une croissance monotone de l’expression:

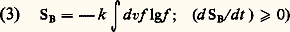
et susceptible dès lors de correspondre à l’entropie d’un état hors d’équilibre (cf. théorie CINÉTIQUE DES FLUIDES). Des recherches ultérieures ont permis d’étendre la portée de cette théorie grâce à la formulation d’équations généralisées dépassant le cadre des gaz dilués (cf. IRRÉVERSIBILITÉ et mécanique STATISTIQUE), et d’élucider les phénomènes de transport, en particulier la théorie linéaire des fluides de densité arbitraire.

La seconde orientation est plus récente et plus ambitieuse car elle correspond à une théorie dynamique de l’irréversibilité, d’où le concept de probabilité serait éliminé au profit d’une interprétation de l’entropie rattachée plus directement aux lois déterministes de la dynamique.

La manifestation d’une extrême sensibilité des trajectoires de l’espace des phases par rapport à leurs conditions initiales, a permis de définir un temps microscopique à partir duquel on peut construire des fonctionnelles non linéaires de l’état statistique, caractérisées par une croissance monotone au cours de l’évolution. Cette propriété permet d’éliminer l’apparente irréductibilité de principe entre la réversibilité des lois de la dynamique et l’irréversibilité des milieux dissipatifs suffisamment complexes. De plus, l’adoption de l’une de ces fonctionnelles comme définition microscopique de l’entropie devient possible. Néanmoins, plusieurs questions préalables restent encore posées, notamment celle de l’unicité d’une telle définition et le lien avec la définition macroscopique. Il semble que ce soit au moyen d’une analyse plus approfondie des mécanismes locaux telle que celle des processus de collisions, et après confrontation avec les acquisitions de la théorie cinétique évoquée plus haut, qu’une définition microscopique générale de l’entropie pourra finalement être établie.

• 1869; formé en all. (Clausius), du gr. entropia « retour en arrière »

♢ Dégradation de l'énergie liée à une augmentation de cette entropie. — Extension de la notion d'entropie à l'informatique.

n. f. PHYS Grandeur thermodynamique S, fonction d'état d'un système, qui caractérise l'état de désordre de celui-ci. (S ne peut pas diminuer au cours d'une transformation d'un système qui n'échange pas de travail avec l'extérieur.)

⇒ENTROPIE, subst. fém.

,,Grandeur thermodynamique exprimant le degré de désordre de la matière`` (Sc. 1962). Loi d'entropie :

• ... quand un ferromagnétique est porté peu à peu vers son point de Curie, son aimantation spontanée (...) diminue de plus en plus rapidement : le désordre s'établit parmi les orientations des moments élémentaires et il en résulte un accroissement d'entropie qui s'ajoute à l'entropie des autres mouvements atomiques.

Hist. gén. des sc., t. 3, vol. 2, 1964, p. 243.

— P. ext., THÉORIE DE L'INFORM. Quantité moyenne d'information attribuable à un message constitué par un ensemble de signaux, représentant le degré d'incertitude où l'on est de l'apparition de chaque signal (d'apr. PIÉRON 1963, Ling. 1972). L'information, c'est l'entropie avec le signe contraire (RUYER, Cybernétique, 1954, p. 46).

Rem. On rencontre ds la docum. entropique, adj. Qui se rapporte à l'entropie (cf. ID., ibid., p. 147). Diagramme entropique. Diagramme où l'on porte en abscisse l'entropie d'un système et en ordonnée la température (cf. Lar. 20^e).

Prononc. :[]. Étymol. et Hist. 1877 (LITTRÉ Suppl.). Prob. empr. à l'all. Entropie « id. » (formé p. anal. avec énergie, à partir du gr. littéralement « action de se retourner » pris au sens de « action de se transformer »), terme proposé en 1850 par le physicien all. R. J. Clausius [1822-1888] cf. 1865 (Pogg. Ann. CXXV, 390 ds NED) pour désigner à l'origine, la quantité d'énergie qui ne peut se transformer en travail. Fréq. abs. littér. :12.

entropie [ɑ̃tʀɔpi] n. f.

ÉTYM. 1877, in Littré, Suppl.; all. Entropie (1850), Clausius, du grec entropia « retour en arrière ».

❖

♦ Phys. En thermodynamique, Fonction définissant l'état de désordre d'un système, croissante lorsque celui-ci évolue vers un autre état de désordre accru. || L'entropie augmente lors d'une transformation irréversible. || Entropie négative. ⇒ Négentropie. || Variation d'entropie d'un système. — Dégradation de l'énergie liée à une augmentation de cette entropie. — Extension de la notion d'entropie à l'informatique.