Akademik

PRÉCESSION ET NUTATION

De même que l’axe d’une toupie qui tourne décrit un cône sous l’action de la pesanteur, l’axe de rotation de la Terre décrit, en 25 800 ans environ, sous l’action des forces d’attraction de la Lune et du Soleil, un cône dont le demi-angle au sommet est de 23⁰ 26 . C’est le phénomène général de la précession . Ainsi, la direction du pôle Nord céleste, actuellement voisine de celle de l’étoile Polaire, en était éloignée de 9⁰ il y a 2 000 ans. Elle sera proche de celle de l’étoile Véga dans 11 000 ans.

Le plan de l’équateur, perpendiculaire à l’axe de la Terre, tourne aussi, de même que l’équinoxe de printemps (ou point 塚), intersection de ce plan avec l’écliptique. Cette direction servant d’origine aux systèmes de coordonnées stellaires, les coordonnées des astres fixes varient elles aussi avec le temps. Ce phénomène a été mis en évidence par Hipparque au II^e siècle avant J.-C., découverte complétée par celles du mouvement de l’écliptique (XVII^e siècle) et de la nutation de Bradley (XVIII^e siècle).

On décompose ce mouvement complexe en deux parties: la précession proprement dite, mouvement continu et actuellement légèrement accéléré de l’axe de la Terre sur un cône de révolution, et la nutation , mouvement multipériodique faisant décrire à cet axe des festons autour du cône (fig. 1).

Calcul de la précession

Les forces d’attraction gravitationnelle du Soleil, de la Lune et des planètes qui s’exercent sur toutes les particules constituant la Terre se décomposent ainsi:

– une force appliquée au centre de gravité de la Terre, qui engendre le mouvement de cette planète dans le système solaire (les forces d’origine planétaire provoquent en particulier le mouvement de l’écliptique);

– les forces s’exerçant de façon différentielle sur des particules qui ne sont pas rigidement liées produisent des déformations du globe (marées terrestres ou océaniques) ou des mouvements des pôles sur notre planète;

– un couple qui crée la précession, la nutation et qui est partiellement responsable du mouvement des pôles; les composantes de ce couple perturbateur dépendent des positions relatives de la Terre, de la Lune et du Soleil, données par la mécanique céleste; ce sont des expressions trigonométriques des périodes de révolution de ces astres, de la période du nœud de l’orbite de la Lune, etc.

Admettons que la Terre soit un corps de révolution dont les moments principaux d’inertie par rapport aux axes choisis sont A , B et C (A = B si l’ellipsoïde terrestre est supposé de révolution) et prenons comme système de référence celui des axes principaux d’inertie, la direction portant C étant orientée vers le pôle Nord. Soit p , q , r les composantes du vecteur vitesse de rotation de la Terre, donc de son axe, et L , M , N celles du couple perturbateur. Le mouvement de précession est régi par les équations d’Euler:

Jusqu’en 1983, les expressions de la nutation utilisées étaient tirées de la théorie de Edgar W. Woolard, qui supposait que la Terre était rigide. À compter du 1^er janvier 1984, l’Union astronomique internationale (U.A.I.) a recommandé l’utilisation des résultats de la théorie de John Wahr, fondée sur un modèle de structure interne de la Terre dû à F. Gilbert et A. M. Dziewonski. Celui-ci prend en compte l’élasticité de la croûte et du manteau et l’existence d’un noyau liquide et d’une graine solide au centre de la Terre.

Expressions de la précession et de la nutation

On appelle équateur moyen un plan qui serait celui de l’équateur si celui-ci ne subissait pas les mouvements périodiques de nutation en opposition avec l’équateur réel ou équateur vrai . Par définition, l’écliptique, plan moyen de l’orbite terrestre, ne subit pas de tels mouvements périodiques.

On reporte sur une sphère (fig. 2) des plans parallèles aux équateurs moyens A¹, A² et aux écliptiques E¹, E² aux instants t ¹ et t ². Les équinoxes correspondants sont 塚¹ et 塚², et les angles 﨎¹ et 﨎² sont les obliquités de l’écliptique.

On appelle M et N, respectivement, les intersections de A¹ avec A² et de E¹ avec E². Enfin, 塚 est l’intersection de A² avec E¹. 祥 = 塚¹ 塚 est la précession luni-solaire. 﨑 = 塚 塚² est la précession planétaire , appelée ainsi parce que le mouvement de l’équinoxe est causé par les planètes. p = 塚²N 漣 塚¹N est la précession générale en longitude . 猪 = 塚²M 漣 塚¹M est la précession générale en ascension droite . Si t est exprimé en années juliennes de 365,25 jours à compter du premier jour julien de l’an 2000 (JJ = 2 451 545), on a:

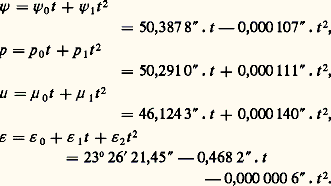
p ⁰ est appelé constante de la précession . En réalité, les termes en t ² ne représentent pas une accélération de la précession, mais sont les premiers termes d’un développement en série entière du temps d’effets à très longue période (plusieurs dizaines de milliers d’années). Une théorie générale valable un temps très long ferait apparaître à leur place ces termes périodiques.

À chaque instant, l’équateur vrai A^v ne coïncide pas avec l’équateur moyen A^m. Les équinoxes correspondants sont 塚^m et 塚^v (fig. 3) et les obliquités 﨎^m et 﨎^v. N = 塚^m 塚^v est la nutation en longitude, 行 = 﨎^v 漣 﨎^m est la nutation en obliquité.

D’après J. Wahr, les termes les plus importants dans l’expression de la nutation sont:

où est la longitude du nœud ascendant de l’orbite lunaire; le terme correspondant, de période 18,6 ans, est la nutation de Bradley ; L est la longitude du Soleil (2 L : période de 6 mois) et l est la longitude de la Lune (2 l : période de 13,66 jours).

Le coefficient 益 de cos dans 行 est la constante de la nutation ( 益 = 9,2025 ).

L’ensemble des termes de la nutation adoptés par l’U.A.I. ainsi que les raisons ayant conduit à leur adoption ont été décrits par P. K. Seidelmann.

Les variations des coordonnées moyennes ou vraies ( 見^m, 見^v: ascension droite; 嗀^m, 嗀^v: déclinaison d’un astre) sont données par:

On se reportera, pour plus de détails, aux travaux d’André Danjon et d’Edgar W. Woolard et Gerald M. Clemence.

Détermination de la précession et de la nutation

Ainsi, la nutation et la précession sont deux aspects d’un même phénomène dont la séparation, fondée sur l’importance des périodes, est tout compte fait assez arbitraire.

Dans le passé, elles étaient déterminées à partir des observations de la position des étoiles. En analysant les variations des coordonnées observées des étoiles en fonction du temps, on déterminait les périodes, les phases et les amplitudes de leurs variations. En particulier, on s’efforçait de préciser l’amplitude du terme de période 18,6 années qui donnait la constante de la nutation. La détermination précise de la précession posait de problèmes plus délicats car d’autres mouvements apparents d’étoiles, ayant aussi un caractère systématique et séculaire, s’y combinent, par exemple la rotation différentielle de la Galaxie, un effet perspectif dû au mouvement du Soleil et une erreur sur le système de référence employé. Ce sont les valeurs déduites de ces observations stellaires qui ont permis d’ajuster les nombres donnés plus haut.

Il est maintenant possible de rattacher l’orientation de la Terre directement à des objets extragalactiques, les quasars, qui constituent, avec une excellente approximation, un repère fixe. La composante céleste du mouvement de rotation de la Terre (cf. TERRE - Mouvements de la Terre ) est ainsi déterminée globalement, de façon continue, par les observations des quasars en radio-interférométrie à longue base (V.L.B.I.). Les valeurs ainsi obtenues sont publiées par le Service international de la rotation terrestre (S.I.R.T., en anglais I.E.R.S., pour International Earth Rotation Service ) sous forme de tables interpolables pour n’importe quel instant et qui incluent à la fois la nutation et tous les aspects de la précession. La précision actuellement obtenue est de l’ordre de 0,000 08 à 0,000 25 pour chaque intervalle de cinq jours.

Pour le moment, la théorie de la précession et de la nutation, malgré des travaux de H. Kinoshita et J. Souchay (1990) et les diverses corrections qu’on a calculées pour passer à un modèle réaliste de la Terre, ne permet pas de décrire la nutation observée avec cette précision. Les tables données par les éphémérides astronomiques sont correctes à 0,002 près et peuvent être utilisées lorsqu’on a besoin d’une précision de cet ordre. Pour les observations précises, il faut utiliser les tables de l’I.E.R.S.

L’analyse des observations V.L.B.I. et des observations de la distance Terre-Lune par laser qui se poursuivent depuis les années 1970 a permis de préciser les valeurs des constantes de la précession et de la nutation (P. Charlot et al., 1991):

Application à la géophysique

Les insuffisances de la théorie de la nutation de Woolard, fondée sur un modèle de Terre rigide, ont été corrigées grâce à la prise en compte de la structure réelle de la Terre. Mais, inversement, c’est parce que la valeur observée de la nutation n’était pas cohérente avec le modèle rigide qu’on a recherché les causes possibles de ces divergences dans la structure de l’intérieur de la Terre. En particulier, l’hypothèse du noyau liquide doit beaucoup aux observations de la nutation.

De plus, il y a une association étroite entre les marées terrestres et la nutation. Produits tous deux par les mêmes forces d’origine luni-solaire, ces deux phénomènes constituent deux aspects de la réaction du globe terrestre à ces sollicitations dynamiques.

Leur étude nous renseigne donc par des voies différentes sur les mêmes paramètres mécaniques de l’intérieur de la Terre. Avec, en plus, l’analyse du mouvement du pôle, les recherches sur la précession et sur la nutation se placent ainsi dans un ensemble plus vaste de travaux destinés à préciser les propriétés mécaniques du globe terrestre.