Akademik

ISOLANTS

On désigne par isolant un matériau qui s’oppose à la transmission d’une forme déterminée d’énergie. On distingue plusieurs types d’isolants selon la nature du processus physique considéré.

Si aucun courant électrique ne circule entre deux conducteurs portés à des potentiels continus différents, le matériau qui les sépare est un isolant électrique . En fait, cet isolant parfait n’existe pas, et une faible intensité circule toujours entre les deux électrodes. Sous tension alternative, il passe un certain courant dans le circuit, en quadrature avec la tension appliquée, mais la puissance dissipée, dans ce cas, au sein de l’isolant est nulle. L’intensité du courant, liée à la géométrie du système, à la tension appliquée et à la fréquence du signal, est proportionnelle à la permittivité du matériau. En pratique, le courant et la tension ne sont jamais rigoureusement en quadrature, et il existe toujours une certaine dissipation d’énergie au sein de l’isolant. Cela peut être dû à la résistivité finie du matériau, mais d’autres types de pertes, comme celles qui résultent de la vibration des dipôles dans le champ électrique, viennent s’y ajouter. Si le champ électrique atteint une valeur élevée, l’isolant peut être perforé par un arc électrique. La valeur du champ électrique correspondant à l’apparition de ce phénomène est la rigidité diélectrique du corps considéré. Selon les applications, c’est-à-dire selon que l’on est en courant continu ou alternatif, que la tension est faible ou élevée, que la fréquence est haute ou basse, on choisit un matériau qui possède de bonnes performances en ce qui concerne l’une ou l’autre des propriétés dont on a besoin.

Si deux corps portés à des températures différentes ne sont l’objet d’aucun échange de chaleur, le milieu qui les sépare est un isolant thermique . Là encore, on distingue plusieurs cas, selon le mode de transmission de l’énergie. Un premier processus est la conduction, c’est-à-dire la transmission de la chaleur par variation progressive de température du matériau intermédiaire. Si celui-ci ne s’échauffe pas dans sa totalité, il s’agit d’un isolant, c’est-à-dire d’un corps de faible conductivité thermique. Il n’existe pas d’isolant susceptible d’empêcher le transport de chaleur par circulation d’un fluide (liquide ou gaz), c’est-à-dire par convection. Les palliatifs consistent à disposer des chicanes et des cloisonnements pour limiter les mouvements de liquides ou de gaz. De même, dans le cas d’un échange de chaleur par rayonnement, la présence d’un écran réfléchissant peut constituer, dans certains cas, une isolation aussi efficace qu’un isolant proprement dit.

En ce qui concerne une transmission d’énergie sous forme de vibration mécanique, par exemple sonore, il est encore plus difficile de parler d’isolants acoustiques , sauf pour certains matériaux absorbants. Dans la majeure partie des cas, c’est un système d’isolation qui sera réalisé pour empêcher tout échange entre deux points. Là encore, des écrans ou divers artifices mécaniques seront souvent plus efficaces que l’interposition d’un matériau isolant au sens propre du terme.

1. Isolants électriques

Propriétés essentielles

Permittivité et résistivité transversale

Un isolant électrique parfait serait un matériau diélectrique parfait. Deux pièces métalliques, séparées par un tel matériau, présenteraient alors une capacité 﨎 fois plus grande que si les deux conducteurs étaient disposés dans le vide. Ce facteur 﨎, appelé permittivité relative, traduit également le rapport des vitesses de propagation d’une onde électromagnétique dans le matériau isolant et dans le vide. Lorsque, dans la suite de ce texte, on parlera de permittivité, il s’agira toujours de sa valeur relative. Rappelons simplement que la valeur absolue serait obtenue en multipliant 﨎 par la permittivité du vide 﨎⁰ égale à 1/(36 神. 10⁹) dans le système international d’unités SI.

Les valeurs de 﨎 pour les divers matériaux sont très variables. Des considérations simples de physique des diélectriques montrent qu’en aucun cas 﨎 ne peut être inférieur à l’unité. Les gaz ont des permittivités très voisines de celle du vide. À titre d’exemple, citons, pour l’hélium, 﨎 = 1,000 066; pour l’oxygène, 﨎 = 1,000 55; pour la vapeur d’eau, 﨎 = 1,006 1. Dans le cas des liquides, la gamme est déjà plus étendue, puisque, pour l’hélium liquide, 﨎 vaut 1,048 à 4,2 K, alors que la permittivité d’une huile de transformateur est de l’ordre de 2,2 et que celle de l’eau atteint 80,5. En ce qui concerne les solides enfin, si pour bon nombre de polymères elle est voisine de 2, pour le verre elle prend des valeurs de l’ordre de 6, et pour certaines céramiques elle peut approcher 1 500.

Si, sous champ électrique modéré, de nombreux isolants ne présentent pas de conductivité mesurable, ce qui est notamment le cas pour les gaz et pour quelques fluides cryogéniques, la plupart d’entre eux sont très légèrement conducteurs, et, entre autres, ils peuvent présenter sous tension alternative des pertes dipolaires, faisant que le courant qui les traverse n’est plus rigoureusement en quadrature avec la tension qui lui donne naissance. L’angle d’erreur correspondant, appelé angle de pertes, puisqu’il traduit une consommation d’énergie active, peut s’interpréter sur un schéma électrique équivalent où le matériau isolant est représenté par une capacité C, avec, en parallèle, une résistance R. Dans ce cas, l’angle de pertes 嗀 est défini par sa tangente:

諸 étant la pulsation du signal appliqué.

Cette valeur de la tangente de l’angle de pertes, appelée également facteur de dissipation diélectrique , dépend étroitement des conditions physiques d’utilisation du matériau isolant. Ainsi, sous tension élevée, s’il apparaît des décharges partielles, c’est-à-dire des ruptures diélectriques locales n’affectant qu’une partie peu importante d’une isolation, elles se traduiront par une augmentation des pertes. D’ailleurs, en fonction de la fréquence et de la température, la valeur de tan 嗀 est susceptible de varier dans de grandes proportions. Dans l’exemple de la figure 1, chacun des maxima correspond à la résonance d’un dipôle particulier.

Dans le schéma équivalent, la valeur de R est donc fonction principalement de la fréquence f ou de la pulsation 諸, de la température T et de la tension appliquée U. En outre, les pertes par conduction peuvent être largement modifiées par différents paramètres extérieurs. Dans certains cas, le transfert de charges peut se faire par l’intermédiaire des molécules mêmes de l’isolant imparfait. Dans d’autres cas, la conduction électronique ou ionique est due en partie à la présence d’impuretés telles que l’eau. De plus, les mobilités variant avec la température, la résistivité transversale peut changer considérablement selon la valeur de ce paramètre.

Résistivité superficielle

Une autre caractéristique importante des isolants est leur résistivité superficielle. Elle traduit la possibilité, pour des charges électriques déposées sur leur surface, que ce soit par frottement ou par décharge, de se déplacer sur cette surface. L’un des facteurs essentiels susceptibles de l’affecter est le degré hygrométrique de l’atmosphère environnante. Des deux valeurs de résistivité, transversale et superficielle, dépendent les propriétés antistatiques du matériau. En effet, si ces deux valeurs sont trop élevées, les charges qui se déposent en surface par un mécanisme quelconque ne s’écoulent que très difficilement, et il peut en résulter une charge électrique locale importante, à tel point que l’intensité du champ électrique à l’extérieur de l’isolant risque, à la limite, de provoquer la rupture diélectrique du milieu extérieur (cf. infra ). On peut, dans la plupart des cas, éviter ce danger soit en abaissant la valeur de la résistivité superficielle par adjonction d’un agent antistatique à la surface du matériau, soit en recourant à des éliminateurs établis le plus souvent sur le principe de l’ionisation de l’air environnant.

Rigidité diélectrique

La dernière des trois propriétés les plus importantes des isolants est la rigidité diélectrique. Là encore, deux cas sont à considérer, du moins pour les solides: la rigidité transversale et la rigidité longitudinale; pour les liquides et les gaz, seule la rigidité transversale a une signification. Elle traduit le phénomène suivant: considérons un matériau dans lequel sont noyées deux électrodes; lorsqu’une tension croissante est appliquée entre ces deux conducteurs, un arc jaillira entre les deux électrodes pour une valeur déterminée de la différence de potentiel. La valeur du champ correspondant est appelée rigidité diélectrique intrinsèque de l’isolant. La formation de cet arc peut avoir des origines très diverses. On se bornera ici à citer, à titre d’exemple, certaines parmi les plus courantes. Dans le cas des gaz, un électron germe, issu le plus souvent d’une électrode sous l’effet du champ électrique, de l’agitation thermique, d’un bombardement électronique ou ionique, est accéléré par ce champ et peut acquérir une énergie suffisante pour ioniser des molécules, qui, libérant ainsi d’autres électrons, produiront un phénomène d’avalanche entraînant la formation d’un pont conducteur entre les électrodes. Le cas des liquides est plus complexe, et plusieurs théories sont encore discutées. Les plus satisfaisantes cependant semblent être celles qui font intervenir comme étape intermédiaire la formation d’une bulle gazeuse, l’arc prenant alors naissance dans cette bulle. En ce qui concerne les solides, l’un des mécanismes les plus courants est lié à l’échauffement local du matériau sous l’effet de ses pertes diélectriques; l’agitation moléculaire qui en résulte abaisse la résistivité, le courant augmente, ce qui accroît la température, et le processus s’accélère jusqu’à constituer un pont conducteur entre les électrodes. Contrairement au cas des gaz ou des liquides, ce mécanisme est irréversible dans les solides, car il entraîne leur perforation.

On a parlé de rigidité diélectrique intrinsèque, c’est-à-dire d’une valeur qui ne dépendrait que du matériau isolant considéré. Dans la pratique, cette valeur est presque impossible à atteindre. En effet, la configuration des lignes de force du champ électrique (qui devrait être parfaitement uniforme), la nature et l’état de surface des électrodes, le volume de matière soumis au champ ont une influence importante. Dans le cas des solides, il est généralement impossible de noyer les électrodes au sein du matériau, et, de ce fait, la nature du milieu et les paramètres physiques extérieurs jouent un rôle déterminant et fort complexe.

Dans bon nombre d’applications à haute tension, la rigidité diélectrique longitudinale des isolants solides peut revêtir une grande importance. Elle concerne le phénomène de contournement, c’est-à-dire la formation d’un arc entre deux électrodes à la surface du matériau sans qu’il soit perforé. La valeur du champ électrique correspondant à la formation de l’arc dépend notamment de la rigidité diélectrique du milieu, des permittivités des deux corps en présence, des formes géométriques des électrodes et de l’isolant, de sa résistivité et de son état de surface.

Utilisations

Les applications des isolants électriques sont extrêmement variées, et, selon les cas, il sera fait appel essentiellement à l’une ou à l’autre de leurs propriétés particulières. Dans les lignes qui suivent, un certain nombre d’exemples permettront de mieux comprendre la façon dont les isolants peuvent être mis en œuvre pour tirer parti au mieux de leurs qualités.

Condensateur pour basse tension

Considérons, en premier lieu, le cas du condensateur pour basse tension utilisé comme composant électronique. Comme, très souvent, l’isolant est soumis à une tension continue, il importe que le matériau choisi ait une résistivité élevée pour s’opposer au passage du courant. Sous champ alternatif, on devra pouvoir le considérer comme une capacité pure, ce qui signifie que ses pertes devront être négligeables aux fréquences et aux températures d’utilisation. De plus, si on veut obtenir une valeur élevée de la capacité, qui, dans le cas le plus fréquent du condensateur plan, est donnée par la relation:

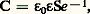
où S est la surface et e l’épaisseur de l’isolant, on voit qu’il est possible d’agir sur trois paramètres. En choisissant un matériau à forte permittivité, comme une céramique, on atteint des valeurs de C considérables, mais les pertes pourront être importantes. Une augmentation de la valeur de S aura comme inconvénient d’accroître le volume du composant. Une diminution de l’épaisseur, par contre, permet une augmentation de la capacité tout en entraînant une miniaturisation du condensateur; mais alors le champ électrique auquel est soumis l’isolant devient plus intense, et la tension limite à laquelle il peut être exposé sans subir de perforation se trouve réduite. Le choix résultera donc d’un compromis entre les divers impératifs qui viennent d’être énumérés, compromis qui sera fonction de l’usage auquel le composant est destiné.

Diélectriques liquides

Les diélectriques liquides sont principalement utilisés dans un triple but.

En premier lieu, par une imprégnation de matériaux fibreux, il est possible de former des complexes possédant des valeurs élevées de rigidité diélectrique transversale. C’est le cas du papier imprégné d’huile minérale qui est très employé dans les transformateurs, les câbles et certains condensateurs.

En deuxième lieu, les échanges thermiques se font plus facilement par l’intermédiaire des liquides que par l’intermédiaire des gaz. Dans les transformateurs, le refroidissement des enroulements se fait essentiellement par une circulation naturelle ou forcée d’huile autour des parties actives. Dans un certain nombre de cas, l’huile est remplacée par des diélectriques chlorés, appelés quelquefois askarels , composés d’un mélange de diphényls chlorés et de trichlorobenzène. Ils présentent sur l’huile l’avantage d’être ininflammables, mais ils ont l’inconvénient d’avoir un pouvoir solvant élevé. De plus, les problèmes écologiques posés par l’utilisation de ces produits les ont fait interdire dans un certain nombre de pays.

Enfin, après la formation d’un arc de rupture, les diélectriques liquides ont un temps de récupération très court, ce qui constitue leur troisième caractéristique, utilisée en particulier dans les disjoncteurs.

Ainsi, dès l’extinction de l’arc, une tension élevée peut sans inconvénient être appliquée de nouveau à l’appareil.

Diélectriques gazeux

C’est surtout dans les disjoncteurs que les diélectriques gazeux sont employés, et cela sous trois formes: gaz sous pression, gaz électronégatifs et gaz très raréfié. On a vu que la rigidité diélectrique d’un gaz est liée au processus de collisions susceptibles d’entraîner la formation d’une avalanche (cf. état GAZEUX). Bien que cela soit très schématique, on conçoit donc facilement qu’en augmentant la pression on réduit le libre parcours moyen des particules et donc l’énergie qu’elles peuvent acquérir dans le champ électrique entre deux collisions successives. Le processus d’avalanche se déclenche pour des valeurs plus élevées du champ électrique: la rigidité diélectrique est accrue.

Dans le cas des gaz électronégatifs, c’est un tout autre mécanisme qui se trouve mis en jeu. Ces gaz, dont le plus utilisé est l’hexafluorure de soufre (SF⁶), ont ceci de particulier que leurs molécules piègent les électrons par lesquels elles sont bombardées, formant ainsi des ions négatifs extrêmement lourds et donc de faible mobilité; on voit ainsi que la rigidité diélectrique peut être très élevée.

La troisième forme de «diélectrique gazeux» est l’atmosphère raréfiée. Réduire la pression d’un gaz entraîne un abaissement de sa rigidité diélectrique, mais cela n’est vrai que jusqu’à une certaine limite. En effet, supposons le cas d’un gaz suffisamment raréfié pour que le libre parcours moyen d’un électron entre deux collisions soit supérieur à la distance entre les deux électrodes. Le déclenchement du processus d’avalanche est impossible, et le mécanisme de rupture est tout à fait différent: il est lié essentiellement aux électrodes, dont la nature, le degré de polissage, la température, la forme géométrique et les traitements préalables (notamment en ce qui concerne les gaz adsorbés) conditionnent la rigidité diélectrique. Par conséquent, entre les pressions usuelles et les vides très poussés, la tension disruptive passe par une valeur minimale qui est fonction de la nature du gaz, de sa pression résiduelle et de l’écartement des électrodes. La représentation graphique des variations de la tension disruptive d’un gaz en fonction du produit de la pression par la distance entre les électrodes est appelée courbe de Paschen (fig. 2). Les propriétés diélectriques très intéressantes du vide ont été peu exploitées, mais il est probable que de nombreuses applications verront le jour dans un proche avenir.

2. Isolants thermiques La transmission de la chaleur

L’énergie thermique se transmet de trois façons différentes, souvent mises en œuvre simultanément. Un premier mode de transmission fait intervenir la conductivité thermique de l’environnement. On reconnaît à ce processus une analogie avec le phénomène de conduction électrique. Supposons en effet une transmission de chaleur par un barreau rectiligne. Si, à un instant donné, T est la température du barreau à l’abscisse x , la quantité de chaleur d Q qui traverse en un temps dt la section du barreau, de surface S, est donnée par la relation:

Le coefficient K ainsi défini est la conductivité thermique du matériau constitutif du barreau. Il ne dépend que de la nature de ce dernier et peut varier dans des proportions relativement grandes. À titre d’exemple, pour le cuivre, il vaut 400 W.m^-1.K^-1 et, pour la laine de verre, 0,04 W.m^-1.K^-1.

Un autre mode de propagation de la chaleur est la convection . Un fluide chauffé est le siège de courants qui apparaissent spontanément (convection naturelle), ou sont engendrés par un moyen artificiel tel que pompe, ventilateur (convection forcée). La chaleur qu’il a accumulée, dont la quantité est liée à sa capacité thermique, est ensuite restituée à un corps à température différente.

Enfin, la chaleur peut se propager par rayonnement . Il s’agit là, en fait, d’un transport d’énergie par onde électromagnétique. Par exemple, la puissance qui nous parvient du Soleil (environ 1 368 W.m^-2 au «sommet» de l’atmosphère) est transmise sous cette forme. Un corps, quel qu’il soit, libère ainsi une énergie qui est fonction de sa température, et il aura donc tendance à se refroidir si aucune énergie ne lui parvient par ailleurs. Dans le cas idéal du «corps noir», c’est-à-dire d’un corps susceptible d’absorber totalement tout rayonnement qui le frappe, quelle qu’en soit la longueur d’onde, la puissance dissipée peut se mettre sous la forme:

où, si W est exprimé en watts, S en mètres carrés et T en kelvins, le coefficient 靖 vaut 5,7 . 10^-8 W.m^-2 K^-4. La longueur d’onde, en mètres, correspondant au maximum d’énergie rayonnée est alors donnée par l’expressionT = 2,9 . 10^-3. Pour les corps réels, dits «colorés» par opposition à l’appellation de corps noir, le coefficient d’absorption ou d’émission varie dans de larges proportions selon la longueur d’onde du rayonnement considéré. Pour une surface métallique polie, par exemple, ce coefficient est négligeable aux températures usuelles dans l’infrarouge. Un tel corps n’émettra donc, par rayonnement, qu’une quantité de chaleur très faible. Pour les matériaux de couleur blanche, le coefficient d’absorption dans le visible est extrêmement réduit, alors que, dans l’infrarouge, il est généralement très grand.

Propriétés des isolants

L’isolant thermique idéal n’existe pas, mais l’isolation doit être conçue selon le mode de transmission de la chaleur que l’on désire principalement freiner.

Dans le cas le plus simple, celui de la convection, il suffit, pour isoler un corps, d’empêcher tout mouvement de fluide autour de lui.

Si, par contre, le processus de conduction est primordial, on disposera, entre la source chaude et la source froide, un matériau de faible conductivité thermique. Le produit considéré devra, le cas échéant, être capable de supporter un gradient de température élevé. C’est ainsi que le verre, dont la conductivité thermique est faible, peut ne pas être utilisable sous forme massive, car le jeu des dilatations différentielles liées au gradient thermique, si ce dernier dépasse un certain seuil, entraînera sa rupture mécanique.

Quant aux pertes par rayonnement, seuls des écrans appropriés sont susceptibles d’en limiter les conséquences. Il ne s’agira donc pas là d’isolants à proprement parler, mais plutôt de systèmes d’isolation, qui, placés autour du corps considéré, lui restitueront une énergie aussi voisine que possible de celle qui aura été rayonnée.

Applications

Aux températures usuelles, de bons résultats peuvent être obtenus avec des isolants poreux. En effet, les conductivités thermiques des gaz ont des valeurs faibles, et le fait d’emprisonner sous forme de bulles un gaz à l’intérieur d’un solide, par lui-même mauvais conducteur de la chaleur, fournit un produit présentant de bonnes performances au point de vue de l’isolation thermique. C’est dans cette catégorie que se classe le liège normal ou sous forme expansée. On l’a remplacé par des matières plastiques expansées, les plus répandues étant le polystyrène, qui peut contenir jusqu’à 97 p. 100 en volume de gaz occlus, et les polyuréthannes. Les matériaux de ce type ont connu un très grand développement à partir du premier choc pétrolier, du fait de leur application à l’isolation thermique des bâtiments à des fins d’économies d’énergie.

Dans le même domaine, la laine de verre est aussi largement utilisée. Elle est constituée de fibres enchevêtrées, de faible diamètre (2 ou 3 micromètres), ce qui conduit à un volume d’air emprisonné important, souvent de l’ordre de 95 p. 100 du volume total.

Une autre solution particulièrement efficace pour l’isolation thermique d’un local consiste à emprisonner de l’air entre deux parois rigides, ce qui permet de réduire considérablement les pertes par conduction et par convection. C’est le cas par exemple des murs doublés par une cloison intérieure disposée à quelques centimètres; c’est le cas aussi des doubles vitrages.

Pour les températures plus élevées, on peut utiliser la laine de verre, jusqu’à quelques centaines de degrés centigrades, et la technique des doubles parois reste valable dans tous les cas. Son efficacité est améliorée si ces parois sont réfléchissantes, car cela permet en effet de limiter les pertes par rayonnement. Pour les très hautes températures, certaines variétés de briques poreuses, ainsi que des produits pulvérulents, comme l’alumine (AL²³) ou la magnésie (MgO) sont d’un emploi courant.

Aux températures cryogéniques, les problèmes d’isolation thermique se posent de façon aiguë, du fait de la faible chaleur de vaporisation de la plupart des gaz liquéfiés, en particulier de l’hélium (dont la température d’ébullition sous pression normale est de 4,2 K). Prenons comme exemple l’isolation d’un cryostat conçu pour l’hélium. Deux techniques, faisant appel à un milieu extrêmement raréfié dont la conductivité thermique est théoriquement nulle, sont possibles. Tous les corps, sauf l’hélium, sont solides à cette température, et leur tension de vapeur est très faible (cf. CRYOLOGIE - Cryophysique). Le phénomène de cryopompage permet d’obtenir, sans grande difficulté, des vides poussés, les pressions résiduelles pouvant être inférieures à 10 ^-5 pascals. Aucun échange par convection n’est possible dans ce milieu. En ce qui concerne les apports de chaleur qui peuvent se faire par rayonnement, on a vu l’intérêt que pouvait présenter l’emploi des métaux polis. On utilisera le plus souvent l’acier inoxydable, qui se polit facilement et qui présente de plus l’avantage d’une mauvaise conductivité thermique, ou bien du verre métallisé. Pour limiter encore l’échauffement qui résulterait du rayonnement, sur le récipient contenant l’hélium liquide, d’une paroi à température ambiante, on interpose, lorsqu’on emploie l’acier inoxydable, un réservoir intermédiaire contenant de l’azote liquide (77 K). De cette façon, le récipient contenant l’hélium ne reçoit le rayonnement que d’une paroi déjà portée à une température très basse.

La seconde technique, plus récente et moins répandue, est celle des superisolations . Elle consiste à remplacer, dans l’enceinte d’isolement sous vide, l’écran à la température de l’azote liquide par des écrans multiples constitués de feuilles minces d’aluminium agissant comme réflecteurs . Ces couches métalliques sont isolées entre elles pour éviter une transmission de chaleur par conduction. Dans la pratique, cela peut être réalisé au moyen de films minces de polytéréphtalate d’éthylène, métallisés et gaufrés pour réduire les surfaces de contact. Une telle technique permet d’atteindre une conductivité thermique équivalente de l’ordre de 10^-5 W.m^-1.K^-1.

3. Isolants acoustiques

La propagation du son

Le son est une vibration mécanique, dont la transmission se fait par une onde de pression, avec une vitesse qui est fonction du milieu. Le son ne se transmet pas dans le vide. Dans un gaz, sa vitesse de propagation, souvent appelée célérité et symbolisée par c , est donnée par la relation: c = ( 塚RTM^-1)^1/2, où R est la constante universelle des gaz, soit 8,31 joules, T la température absolue, 塚 le rapport des chaleurs spécifiques à pression et à volume constants, et M la masse molaire. Dans les solides, la célérité d’une onde longitudinale est sensiblement donnée par: c = (E 福^-1)¹², E étant le module d’élasticité du matériau et 福 sa densité.

Lorsqu’une onde sonore passe d’un milieu à un autre, une partie seulement de l’énergie est transmise, l’autre est réfléchie à l’interface entre les deux corps. Si l’on désigne par Z = 福c l’impédance acoustique spécifique du premier milieu et par Z celle du second, et si l’on pose m = Z /Z, le rapport 倫 de l’intensité du signal réfléchi à celle du signal incident s’exprime:

et 淪, celui de l’intensité du signal transmis au signal incident, est donné par:

On peut constater que le fait de changer m en 1/m ne modifie pas les valeurs de 倫 et de 淪. Cela signifie que les intensités des ondes réfléchies et transmises seront les mêmes, que le signal se déplace d’un milieu 1 vers un milieu 2 ou vice versa.

Lors de la propagation d’une vibration mécanique, les mouvements produits causent des frottements, et donc une dissipation d’énergie au sein du matériau. Il en résulte un affaiblissement de l’intensité du signal sonore (énergie traversant l’unité de surface par unité de temps), de telle sorte qu’un signal d’intensité initiale I⁰ n’a plus, après avoir parcouru une distance x , qu’une intensité:

見 étant le coefficient d’absorption du milieu, fonction de la fréquence. Dans le cas d’une onde sphérique, l’intensité décroît, de plus, comme l’inverse du carré de la distance.

Exemples d’isolations

Une première solution d’isolation consiste à empêcher une vibration de se propager à partir de la source qui lui donne naissance. Prenons l’exemple d’une machine tournante (moteur, alternateur...). On peut, en premier lieu, arrêter la transmission vers le sol de l’onde mécanique en interposant des ressorts qui, judicieusement calculés, jouent le rôle de filtre passe-bas. Leur efficacité sera améliorée en les doublant de dash-pots , c’est-à-dire d’amortisseurs constitués, par exemple, de cylindres remplis d’huile, dans lesquels le déplacement d’un piston engendre un frottement, et donc un amortissement de la vibration. Les amortisseurs peuvent quelquefois être remplacés par des matériaux qui, en plus d’une certaine élasticité, possèdent des frottements internes propres assez considérables, tels que le liège aggloméré, le feutre, le caoutchouc, le plomb et des matières plastiques expansées ou non. Pour atténuer les sons transmis par l’air, une solution consiste à entourer la machine avec de tels matériaux, par exemple en tapissant son enveloppe. Pour réduire encore le niveau sonore du local, il est souhaitable de limiter la réflexion des ondes sur les parois. Pour cela, l’un des procédés les plus efficaces est l’installation de panneaux percés de trous à une certaine distance des murs. En choisissant convenablement la nature du panneau, son nombre de trous par unité de surface, sa distance à la paroi, et en interposant éventuellement un matériau absorbant entre les deux, on peut réaliser une impédance acoustique voisine de celle de l’air, de telle sorte que le coefficient de réflexion soit nul.

La seconde solution d’isolation consiste à empêcher les bruits de parvenir en un lieu déterminé. Pour cela, il convient, comme dans le cas précédent, d’éviter la propagation par le sol aussi bien que par l’air. Dans le premier cas, on dispose généralement des matériaux absorbants, par exemple le liège aggloméré, les laines de verre et de roche, ou, de plus en plus, des mousses de matières plastiques (notamment polystyrène ou polyuréthanne). En ce qui concerne la transmission par l’air, l’épaisseur des murs est un facteur déterminant de l’insonorisation des locaux. Cependant les ouvertures, les vitres en particulier, ont une influence importante, et il est bon de mettre un double vitrage avec un matelas d’air entre les deux. Signalons, pour montrer les difficultés d’un tel problème, qu’une ouverture de 5 mm au bas d’une porte peut transmettre autant d’énergie que la porte elle-même.