- МЕХАНИКА ТЕЛ ПЕРЕМЕННОЙ МАССЫ
-
раздел теор. механики, в к-ром изучается движение матер. тел, масса к-рых изменяется во время движения. Осн. исследования по М. т. п. м. принадлежат И. В. Мещерскому и К. Э. Циолковскому. Задачи М. т. п. м. выдвигаются развитием авиационной и ракетной техники, а также теор. механики и астрономии.Изменение массы тела (точки) во время движения может обусловливаться отделением (отбрасыванием) ч-ц или их присоединением (налипанием). При полёте совр. реактивных самолётов с воздушно-реактивными двигателями происходят одновременно как процессы присоединения, так и отделения ч-ц. Масса таких самолётов увеличивается за счёт ч-ц воздуха, засасываемых в двигатель, н уменьшается в результате отбрасывания ч-ц — продуктов горения топлива. Основное векторное дифф. ур-ние движения точки перем. массы для случая присоединения и отделения ч-ц, полученное в 1904 Мещерским, имеет вид: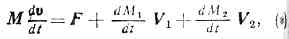 где М — масса точки, v — её скорость, t — время, F — равнодействующая приложенных сил, V1 — относит. скорость отделяющихся ч-ц, ?dM1/dt? секундный расход массы, V2 — относит. скорость присоединяющихся ч-ц, ?dM2/dt? — секундный приход массы. Произведение (dM1/dt)V1=Ф1—реактивная тяга, a ( dM2/dt)V2=Ф2— тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние движения получается из (*) при условии, что Ф2=0.В М. т. п. м. рассматриваются два класса задач: определение траектории центра масс и определение движения тела перем. массы около центра масс. В ряде случаев можно найти траекторные хар-ки движения центра масс, исходя из ур-ний динамики точки перем. массы. Изучение движения тел перем. массы около центра масс важно для исследования динамич. устойчивости реальных объектов (ракет, самолётов), их управляемости и манёвренности. К задачам М. т. п. м. относится также отыскание оптим. режимов движения, т. е. определение таких законов изменения массы тела или точки, при к-рых кинематич. или динамич. хар-ки их движения становятся наилучшими. Наиболее эфф. метод решения таких задач — вариационное исчисление.Важной задачей механики тел перем. массы с тв. оболочкой явл. изучение движения этих тел при нек-рых дополнит. условиях, налагаемых на скорость центра масс. Такие задачи возникают, напр., при изучении движения телеуправляемых ракет и беспилотных самолётов, наводимых на цель автоматически, или по радиокомандам с Земли, или же по командам, вырабатываемым головками самонаведения. Большое число работ по М. т. п. м. относится к изучению движения небесных тел. Допуская, что увеличение массы небесного тела происходит за счёт налипания косм. пыли, приходят к дополнит. условию о равенстве нулю абс. скорости налипающих ч-ц. Ур-ние движения точки перем. массы в этом случае принимает вид: d/dt(Mv)=F. М. т. п. м. находит приложения при исследованиях и в др. областях техники.
где М — масса точки, v — её скорость, t — время, F — равнодействующая приложенных сил, V1 — относит. скорость отделяющихся ч-ц, ?dM1/dt? секундный расход массы, V2 — относит. скорость присоединяющихся ч-ц, ?dM2/dt? — секундный приход массы. Произведение (dM1/dt)V1=Ф1—реактивная тяга, a ( dM2/dt)V2=Ф2— тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние движения получается из (*) при условии, что Ф2=0.В М. т. п. м. рассматриваются два класса задач: определение траектории центра масс и определение движения тела перем. массы около центра масс. В ряде случаев можно найти траекторные хар-ки движения центра масс, исходя из ур-ний динамики точки перем. массы. Изучение движения тел перем. массы около центра масс важно для исследования динамич. устойчивости реальных объектов (ракет, самолётов), их управляемости и манёвренности. К задачам М. т. п. м. относится также отыскание оптим. режимов движения, т. е. определение таких законов изменения массы тела или точки, при к-рых кинематич. или динамич. хар-ки их движения становятся наилучшими. Наиболее эфф. метод решения таких задач — вариационное исчисление.Важной задачей механики тел перем. массы с тв. оболочкой явл. изучение движения этих тел при нек-рых дополнит. условиях, налагаемых на скорость центра масс. Такие задачи возникают, напр., при изучении движения телеуправляемых ракет и беспилотных самолётов, наводимых на цель автоматически, или по радиокомандам с Земли, или же по командам, вырабатываемым головками самонаведения. Большое число работ по М. т. п. м. относится к изучению движения небесных тел. Допуская, что увеличение массы небесного тела происходит за счёт налипания косм. пыли, приходят к дополнит. условию о равенстве нулю абс. скорости налипающих ч-ц. Ур-ние движения точки перем. массы в этом случае принимает вид: d/dt(Mv)=F. М. т. п. м. находит приложения при исследованиях и в др. областях техники.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МЕХАНИКА ТЕЛ ПЕРЕМЕННОЙ МАССЫ
-
- раздел теоретич. механики, изучающий движение материальных тел, масса к-рых изменяется во время движения. Осн. исследования по M. т. п. м. принадлежат И. В. Мещерскому и К. Э. Циолковскому. Задачи M. т. п. м. возникли в связи с развитием авиационной и ракетной техники, а также теоретич. механики и астрономии. Частной задачей M. т. п. м. является движение тел с пост, массой, но перем. моментом инерции. Изменение массы тела (точки) во время движения может обусловливаться отделением (отбрасыванием) частиц или их присоединением (налипанием). При полёте совр. реактивных самолётов с воздушно-реактивными двигателями происходят одноврем. процессы как присоединения, так и отделения частиц. Масса таких самолетов увеличивается за счёт воздуха, засасываемого в двигатель, и уменьшается в результате отбрасывания продуктов горения топлива. Осн. векторное дифференц. ур-ние движения точки перем. массы для случая присоединения и отделения частиц, полученное в 1904 Мещерским, имеет вид
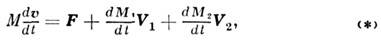
где M- масса точки,
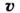 - её скорость, t- время,
- её скорость, t- время, 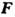 - равнодействующая приложенных сил,
- равнодействующая приложенных сил,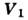 - относит, скорость отделяющихся частиц,
- относит, скорость отделяющихся частиц,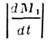 - секундный расход массы,
- секундный расход массы,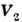 - относит, скорость присоединяющихся частиц,
- относит, скорость присоединяющихся частиц,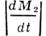 - секундный приход массы. Произведение
- секундный приход массы. Произведение 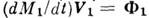 - реактивная тяга, а
- реактивная тяга, а 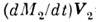 =
=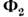 - тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние движения получается из (*) при условии, что
- тормозящая сила, обусловленная присоединением частиц. Для совр. ракет ур-ние движения получается из (*) при условии, что 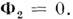
В M. т. п. м. рассматриваются два класса задач: определение траектории центра масс и определение движения тела перем. массы около центра масс. В ряде случаев можно найти траекторные характеристики движения центра масс, исходя из ур-ний динамики точки перем. массы. Изучение движения тел перем. массы около центра масс важно для исследования динамич. устойчивости реальных объектов (ракет, самолётов), их управляемости и манёвренности. К задачам M. т. п. м. относится также отыскание оптим. режимов движения, т. е. определение таких законов изменения массы тела или точки, при к-рых кинематич. или динамич. характеристики их движения становятся наилучшими. Наиб, эфф. методы решения таких задач - методы вариационного исчисления.
Важной задачей M. т. п. м. с твёрдой оболочкой является изучение движения этих тел при нек-рых дополнит, условиях, налагаемых на скорость центра масс. Такие задачи возникают, напр., при изучении движения телеуправляемых ракет и беспилотных самолётов, наводимых на цель автоматически или по радиокомандам с Земли, или по командам, вырабатываемым головками самонаведения. Для зенитных управляемых ракет и ракет класса "воздух - воздух" (предназначенных для стрельбы с самолёта по самолёту) процесс изменения массы происходит, как правило, на всей траектории полёта.
Большое число работ по M. т. п. м. относится к изучению движения небесных тел. Допуская, что увеличение массы небесного тела происходит за счёт налипания космич. пыли, приходят к дополнит, условию о равенстве нулю абс. скорости налипающих частиц. Ур-ние движения точки перем. массы в этом случае принимает вид
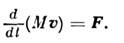
Интерполируя реальные законы изменения массы небесных тел простыми алгебраич. ф-циями времени ("законы Мещерского"), можно аналитически исследовать движение точки перем. массы в поле центральной силы. Мещерскому принадлежит постановка обратных задач M. т. п. м., в к-рых определяется закон изменения массы точки по нек-рым заданным свойствам наблюдаемого движения в известном поле сил.
Для нек-рых задач небесной механики Мещерский указал такие преобразования переменных (координат и времени), при помощи к-рых ур-ния точки перем. массы переходят в ур-ния точки пост, массы (в новом пространстве-времени). M. т. п. м. находит приложение при исследованиях и в др. областях, напр, в текстильной промышленности и радиолокации.
Лит.: Мещерский И. В., Работы по механике тел переменной массы, 2 изд., M., 1952; Циолковский К. Э., Собр. соч., т. 2, M., 1954; Михайлов Г. К., К истории динамики систем переменного состава и теории реактивного движения, M., 1974; Гродзовский Г. Л., Иванов Ю. H., Токарев В. В., Механика космического полета, M., 1975; Акуленко Л. Д., Асимптотические методы оптимального управления, M., 1987. А. А. Космодемьянский.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.