Akademik

форсинг-метод,- особый способ доказательства существования моделей аксиоматич. теорий, предложенный П. Козном в 1963 для доказательства совместимости отрицания континуум-гипотезы щСН и других теоретико-множественных предложений с аксиомами системы Цермело - Френкеля ZF (см. [1]). В дальнейшем В. м. был упрощен и модернизирован (см. [2]-[6]); выявилась, в частности, связь этого метода с теорией булееозначных моделей (см. [2), [3]) и моделями Крипке (см. [6]).

Центральным понятием В. м. является отношение вынуждения

("условие рвынуждает формулу ").

Определению отношения вынуждения предшествует фиксирование нек-рого языка Lи частично упорядоченного множества Рвынуждающих условий р с отношением порядка . Язык Lможет содержать переменные и константы разных сортов (или типов).

Построение модели ZF, предложенное П. Козном, в к-рой нарушается континуум-гипотеза, выглядит следующим образом. Множество Мназ. транзитивным, если

Пусть М - счетное транзитивное множество, являющееся моделью ZF, и - ординальное (по Нейману) число, т. е. Пусть - произвольное множество (возможно, что ), где - первое бесконечное ординальное число. Если X - транзитивное множество, то пусть Def (X).обозначает множество всех X-определимых подмножеств (см. Конструктивное по Гёделю множество), т. е. .С помощью процесса, аналогичного построению конструктивных по Гёделю множеств, для каждого ординального числа , дуктивно определяется множество :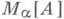

Пусть где : 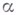- ординал . Модель ZF, в к-рой нарушается континуум-гипотеза, ищется среди моделей вида М[А]. Пусть - ординал такой, что в Мистинно утверждение: есть второй несчетный ординал.

Множество вынуждающих условий Ри отношение определяются эквивалентностями: а) -функция, определенная на век-ром конечном подмножестве множества , со значениями в множестве ) есть продолжение р. В качестве языка Lберется так наз. разветвленный язык, имеющий много типов переменных (для каждого свой тип переменных, пробегающих множество ) и содержащий имена (т. е. индивидные константы) для каждого множества из . Если , то имя хобозначается через . Пусть а - имя множества А. Отношение вынуждения вводится индуктивным определением, имеющим, в частности, следующие характерные пункты:

Если - тип переменной х, то

где - множество всех констант типа 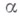. Последовательность вынуждающих условий

наз. полной, если для всякой замкнутой формулы 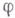языка Lимеет место

Счетность множества всех замкнутых формул языка Lи пункт (2) определения отношения вынуждения позволяют доказать существование полной последовательности, начиная с любого р ₀ .

Множество А, содержащееся в , наз. генерическим относительно модели М, если существует такая полная последовательность, что есть характеристич. функция множества А. Фундаментальное значение имеют следующие два факта о генерических множествах и отношении вынуждения .

I. Если А - генернческое множество, то

где означает, что формула истинна в М[А].

II. Отношение

где 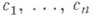- константы L, рассматриваемое как отношение между р, c₁ ,..., с _n выразимо в модели М.

В силу этих фактов, для доказательства того, что М[A]| = j, достаточно показать истинность в модели Мутверждения

На этом основана проверка справедливости в модели М[А]аксиом ZF и . При проверке в используется также специфика множества вынуждающих условий, позволяющая доказать, что:

1) если ординалы 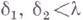различны, то

т. е.

2)

Укажем, как отношение вынуждения связано с булевозначными моделями.

Если ввести обозначения

то есть полная булева алгебра и есть булево значение формулы . Таким образом, задание частично упорядоченного множества и определение отношения оказываются равносильными построению нек-рой булевозначной модели . Анализ доказательства утверждений вида:

где - аксиома или , позволяет заключить, что формулы 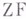, выражающие утверждение:

т. е. 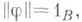выводимы из аксиом . Таким образом, есть B-модель для , построенная средствами ZF. Предположение о существовании счетного транзитивного множества, являющегося моделью ZF, равно как и понятие генерического множества, оказываются несущественными для целей доказательства относительной непротиворечивости.

Выяснилось, что построение булевозначной модели можно упростить (см. [2], [3], [5]). В частности, введение разветвленного языка Lне является обязательным. Возможен следующий способ построения генерической модели М[А](см. [4]).

Подмножество Xчастично упорядоченного множества наз. плотным, если

Пусть Ри отношение суть элементы нек-рого счетного транзитивного множества М, являющегося моделью ZF. Подмножество наз. M-генерическим фильтром, если:

Пусть Gесть Л/-генернческий фильтр на Р. Так как Мсчетно, то Gсуществует. Вообще говоря, . Отношение определяется эквивалентностью

где хи у - произвольные элементы модели М. Пусть функция определена на Мравенством

и

Если - замкнутая формула языка ZF, пополненного константами для обозначения каждого множества из М, то положим (G есть М-генерический фильтр ) Можно показать, что

I.

II. Отношение определимо в модели Мдля каждой формулы .

Используя только I, II и тот факт, что М - модель ZF, можно установить, что NQ - модель ZF. Если Ропределено эквивалентностями (а).и (6), то и есть характеристич. функция нек-рого множества п . Определимое в Мотношение не удовлетворяет пунктам (3) и (5) определения П. Коэна отношения вынуждения. Имеет место

Полагая

получим определимую в Мбулевозначную модель для с той же булевой алгеброй , что и в случае П. Коэна.

Таким образом, В. м. состоит фактически в построении В-модели и гомоморфизма, сохраняющего нек-рые бесконечные объединения и пересечения алгебры , в двухэлементную алгебру (о применениях В. м. в теории множеств см., напр., [2]).

Лит.:[1] Коэн П. Д ж., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; [2] И е х Т., Теория множеств и метод форсинга, пер. с англ., М., 1973; [3] Тakеuti G., Zaring W. M., Axiomatic Bet theory, N. Y. - Hdlb. - B., 1973; [4] Шенфилд Д ж., Математическая логика, пер с англ., М., 1975; [5] Манин Ю. И., в кн.: "Итоги науки к техники. Современные проблемы математики, т. 5, М., 1975 с. 5-72; [6] Fitting M. С., Intuitionistic logic, model theory and forcing, Amst.- L., 1969. В. Н. Гришин.