Akademik

- одна из краевых задач для дифференциальных уравнений с частными производными. Пусть, напр., в ограниченной области , в каждой точке границы Г к-рой существует нормаль, задано эллиптич. уравнение 2-го порядка

где В. к. з. для уравнения (*) в области наз. следующая задача: из множества всех решений уравнения (*) требуется выделить те, к-рые в каждой граничной точке имеют производные по внутренней конормали N и удовлетворяют условию

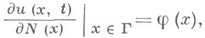
где j(x) - заданная функция. В. к. з. наз. также задачей Неймана.

Лит.:[1] Бицадзе А. В., Краевые задачи для эллиптических уравнении второго порядка, М., 1966; [2] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [3] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [4] Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961. А. К. Гущин.