Akademik

одно из основных возможных (наряду С Шрёдингера представлением и с Гейзенберга представлением).эквивалентных представлений зависимости от времени tоператоров А и волновых функций 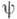в квантовой механике и квантовой теории поля. Квантовую систему с учетом взаимодействия между ее частями (в квантовой механике) или составляющими ее различными полями (в квантовой теории поля) можно описать в представлении Шрёдингера с помощью Шрёдингера уравнения:

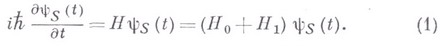
Предполагается, что полный гамильтониан Нразделяется на гамильтониан свободных (невзаимодействующих) частей или полей 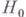и гамильтониан взаимодействия . Гамильтонианы и являются некоммутирующими (иначе задача становится тривиальной, так как разбиение гамильтониана на и теряет смысл) функциями операторов, соответствующих различным свободным полям и не зависящих от времени в представлении Шрёдингера. Унитарное преобразование

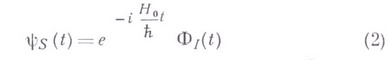
осуществляет переход к В. п., где волновая функция удовлетворяет уравнению:

т. е. зависимость 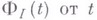определяется гамильтонианом взаимодействия в представлении

При этом среднее значение оператора Ав представлении Шрёдингера

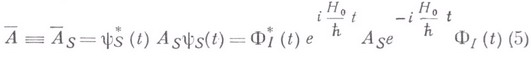
можно также понимать как среднее значение по волновым функциям от оператора А _I в В. п.

В В. п. операторы, соответствующие физическим динамич. величинам, зависят от времени согласно (6) как операторы в представлении Гейзенберга для свободных нолей, а изменение волновых функций с течением времени tопределяется эффектами взаимодействия между полями. При описании поведения квантовой системы с течением времени tВ. п. позволяет выделить зависимость от гамильтониана свободных полей Н ₀ , к-рую обычно легко определить, и сосредоточить внимание на исследовании уравнений (3) и (4), содержащих всю информацию о взаимодействии между полями. Особенно удобно использовать В. п. в случае, когда H₁ содержит нек-рый малый параметр и соответствующие решения можно искать по теории возмущений в виде рядов по степеням этого малого параметра.

Свойство инвариантности средних значений (5), к-рые должны быть наблюдаемыми и иметь тем самым физич. смысл относительно унитарных преобразований (2) и (6), означает эквивалентность В. п. и представлений Шрёдингера и Гейзенберга. в. д. Куцин.