Akademik

- модель ветвящегося процесса (с дискретным пли непрерывным временем, с одним или несколькими типами частиц и т. д.), в к-рой новые частицы могут появляться не только при делении частиц, но и в результате иммиграции из какого-то "внешнего источника". Напр., пусть

- независимые случайные величины с производящими функциями

соответственно; тогда ветвящийся Гальтона-Ватсона процесс с иммиграцией можно задать соотношениями (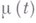 - число частиц): и

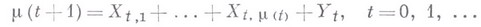
(величина 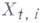интерпретируется как размер потомства i-й частицы t-го поколения, величина 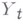-как число частиц, иммигрирующих в t-e поколение). Производящие функции

определяются рекуррентными соотношениями

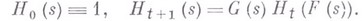
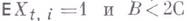Соответствующая ветвящемуся процессу Гальтона-Ватсона с иммиграцией цепь Маркова возвратна, если или и невозвратна, если или 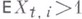. Для эргодичности цепи Маркова 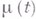, т. е. для того чтобы существовали пределы

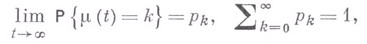
необходимо и достаточно (см. [3]), чтобы

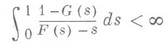
(это условие выполняется, в частности, если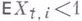

и ). Если 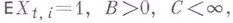то (см. [4]):

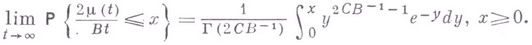
Если то (см. [5]) существует такая последовательность чисел 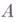, что

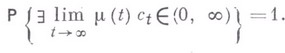
Для В. п. с и., в к-рых иммиграция происходит только при 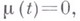т. е.

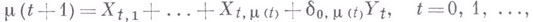
где 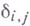- символ Кронекера, при и справедливо соотношение,

Лит.: [1] Зубков А. М., "Теория вероят. и ее примен.", 1972, т. 17, в. 1, с. 179-88; [2] Pakes A. G., "J. Austral. Math. Soc.", 1972, v. 13, № 3, p. 277-90; [3] Foster J. H., Williams о n J. A., "Z. Wahrscheinlichkeitstheor. und verw. Geb.", 1971, Bd 20, №3, S. 227-35; [4] Seneta E., "J. Roy. Statist. Soc.", 1970, v. 32, № 1, p. 149-52; [5] его же, "Math. Biosci.", 1970, v. 7, № 1, p. 9-14; [6] Foster J. H., "Ann. Math. Statistics", 1971, v. 42, № 5, p. 1773-6.

А. М. Зубков.