Akademik

характеристики множеств на прямой. Верхняя грань нек-рого множества действительных чисел - наименьшее число, ограничивающее сверху это множеетво. Нижняя грань данного множества - наибольшее число, ограничивающее его снизу. Более подробно: пусть задано нек-рое подмножество Xдействительных чисел. Число b наз. его верхней гранью (в. 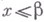г.) и обозначается sup X(от латинского слова supremum - наивысшее), если для каждого числа выполняется неравенство , и каково бы ни было существует такое , что . Число наз. нижней гранью (н. 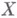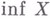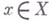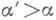г.) множества п обозначается (от латинского слова infimum - наинизшее), если для каждого выполняется неравенство , и каково бы ни было существует такое , что

Примеры:

если множество Xсостоит из двух точек 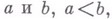то

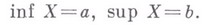
Эти примеры показывают, в частности, что в. г. (н. г.) может как принадлежать этому множеству (напр., в случае отрезка 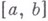), так и не принадлежать ему (напр., в случае интервала ). Если в нек-ром множестве существует наибольшее (наименьшее) число, то оно, очевидно, и является в. г. (н. г.) этого множества.

В. г. (н. г.) не ограниченного сверху (снизу) множества наз. символ (соответственно символ ).

Если N - множество натуральных чисел: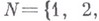 то

Если 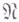множество всех целых чисел, положительных и отрицательных, то

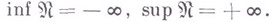
Всякое непустое множество действительных чисел имеет и притом единственную в. г. (н. г.) конечную или бесконечную. При этом всякое ограниченное сверху непустое множество имеет конечную в. г., а всякое ограниченное снизу - конечную н. г.

Иногда в. г. (н. г.) множества наз. его точной верхней (нижней) гранью, понимая в этом случае под термином в. г. (н. г.) множества любое число, ограничивающее его сверху (снизу). Реже, вместо термина в. г. (н. г.) множества, в том или ином из вышеуказанных смыслов, употребляется термин верхняя (нижняя) граница множества. В. г. (н. г.) функции, принимающей действительные значения, в частности последовательности действительных чисел, называют в. г. (н. г.) множества ее значений.

Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд.. ч. 1, М., 1971; [2] Кудрявцев Л. Д.. Математический анализ, 2 изд., т. 1, М., 1973; [3] Никольский С. М., Куре математического анализа, т. 1, М., 1973. Л. Д. Кудрявцев.