следовая норма,- норма в пространстве N(X, Y) ядерных операторов, отображающих банахово пространство Xв банахово пространство Y.
Пусть X, Y - банаховы пространства над полем действительных или комплексных чисел, L(X, Y) - пространство всех непрерывных линейных операторов, отображающих Xв Y, F(X, Y) - линейное подпространство, состоящее из операторов конечного ранга (т. е. операторов с конечномерным образом). Банахово сопряженное пространство к Xобозначается X', значение функционала 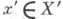 на векторе
на векторе  обозначается <x, х'>.
обозначается <x, х'>.
Каждый ядерный оператор  допускает представление в виде
допускает представление в виде

где {x'i}и {yi} - такие последовательности в X' и Y соответственно, что

такие представления наз. ядерными. Величина

где точная нижняя грань берется по всевозможным ядерным представлениям вида (1), наз. ядерной нормой оператора А. Эта норма превращает N(X, Y) в банахово пространство, к-рое содержит F(X, Y) в качестве плотного линейного подпространства. Если  то сопряженный оператор А' содержится в N'(Y, X' )и
то сопряженный оператор А' содержится в N'(Y, X' )и 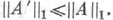 Пусть
Пусть  - обычная операторная норма в L(X, Y). Тогда
- обычная операторная норма в L(X, Y). Тогда 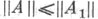 для всех
для всех  Если
Если 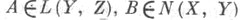 , то
, то 
 и
и 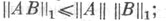 если
если 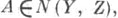
 то
то 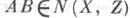 и
и  Любой оператор
Любой оператор 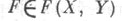 представим в виде
представим в виде

Величина 
где точная нижняя грань берется по всевозможным конечным представлениям вида (3), наз. конечной ядерной нормой оператора F. Пространство F(X, Y )можно отождествить с тензорным произведением  При этом оператору Fвида (3) соответствует элемент
При этом оператору Fвида (3) соответствует элемент

и конечная Я. н. (4) переходит в норму 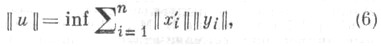
где точная нижняя грань берется по всем конечным представлениям элемента ив виде (5). Эта норма наз. тензорным (или скрещенным) произведением норм в Y и в X'. Пополнение  по норме (6) обозначается
по норме (6) обозначается  Отображение
Отображение 
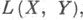 при к-ром элемент (5) переходит в оператор (3), продолжается до непрерывного линейного оператора
при к-ром элемент (5) переходит в оператор (3), продолжается до непрерывного линейного оператора  Образ оператора Г совпадает с N( Х, Y). Если отображение Г устанавливает взаимно однозначное соответствие между
Образ оператора Г совпадает с N( Х, Y). Если отображение Г устанавливает взаимно однозначное соответствие между  и N(X, Y), тo(X, Y )совпадает с замыканием F(X, Y) по норме (4); в этом случае сужение Я. н. на F(X, Y) совпадает с конечной Я. н. Однако в общем случае оператор Г может иметь нетривиальное ядро, так что Я. н. является результатом факторизации нормы в
и N(X, Y), тo(X, Y )совпадает с замыканием F(X, Y) по норме (4); в этом случае сужение Я. н. на F(X, Y) совпадает с конечной Я. н. Однако в общем случае оператор Г может иметь нетривиальное ядро, так что Я. н. является результатом факторизации нормы в  (см. Ядерный оператор).
(см. Ядерный оператор).
Пусть X=Y=H, где H - сепарабельное гильбертово пространство; L(H)=L(H, Н)- алгебра ограниченных операторов в Н, L1(H)=N(H, Н)- идеал ядерных операторов в L(H). В этом случае отображение Г взаимно однозначно, для операторов конечного ранга Я. н. совпадает с конечной Я. н. и каждый оператор  имеет след trA(см. Ядерный оператор). Я. н. оператора
имеет след trA(см. Ядерный оператор). Я. н. оператора  совпадает с величиной
совпадает с величиной  где А *- сопряженный к Аоператор в H. Я. н. связана с Гильберта-Шмидта нормой
где А *- сопряженный к Аоператор в H. Я. н. связана с Гильберта-Шмидта нормой 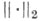 неравенством
неравенством  Общий вид линейного непрерывного функционала в банаховом пространстве L1(H) дается формулой
Общий вид линейного непрерывного функционала в банаховом пространстве L1(H) дается формулой
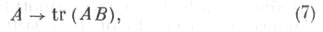
где В - произвольный оператор из L(Н). причем норма функционала (7) совпадает с ||B||. Следовательно, L(H)изометрично пространству, сопряженному к L1(H). Формула (7) дает общий вид линейного функционала и на замкнутом подпространстве  в L(H), состоящем из всех вполне непрерывных (компактных) операторов; при этом
в L(H), состоящем из всех вполне непрерывных (компактных) операторов; при этом 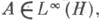 а Впробегает Ll(H). При этом норма функционала (7) совпадает с
а Впробегает Ll(H). При этом норма функционала (7) совпадает с 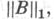 т. е. пространство ядерных операторов L1(H)с Я. н. изометрично пространству, сопряженному к
т. е. пространство ядерных операторов L1(H)с Я. н. изометрично пространству, сопряженному к  в обычной операторной норме. Перечисленные результаты допускают нетривиальные обобщения на случай операторов в банаховых пространствах.
в обычной операторной норме. Перечисленные результаты допускают нетривиальные обобщения на случай операторов в банаховых пространствах.
Пример. Пусть X=Y=ll - пространство суммируемых последовательностей. Оператор  содержится в N(l1,l1 )тогда и только тогда, когда существует такая бесконечная матрица
содержится в N(l1,l1 )тогда и только тогда, когда существует такая бесконечная матрица  что A переводит последовательность
что A переводит последовательность  и
и  В этом случае
В этом случае 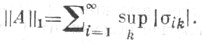
Лит.:[1] Grothendieck Л., Froduits tensoriels topologiques et espaces nucleaircs, Providence, 1955; [2] Пич А., Операторные идеалы, пер. с англ., М., 1982; [3] его же, Ядерные локально выпуклые пространства, пер. с нем., М., 1967; [4] Гохберг И. Ц., Крейн М. Г., Введение в теорию линейных несамосопряженных операторов в гильбертовом пространстве, М., 1965; [5] Гельфанд И. М., Виленкин Н. Я., Некоторые применения гармонического анализа. Оснащенные гильбертовы пространства, М., 1961; [6] Морен К., Методы гильбертова пространства, пер. с польск., М., 1965; [7] Дэй М., Нормированные линейные пространства, пер. с англ., М., 1961.
Г. Л. Литвинов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.